搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．计算：
=（）
=（）A． | B． | C． | D． |
2．下列运算正确的是（）
A． | B． |
C． | D． |
3．用3个完全相同的小正方体组成如图所示的几何体，则它的俯视图是（ ）
A． | B． | C． | D． |
4．一个不透明的布袋中，放有3个白球，5个红球，它们除颜色外完全相同，从中随机摸取1个，摸到红球的概率是（ ）
A． | B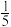． | C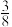． | D． |
5．直线y=2x－4与y轴的交点坐标是( )
| A．(4，0) | B．(0，4) | C．(－4，0) | D．(0，－4) |
6．在正方形、矩形、菱形、平行四边形、等腰梯形中，其中中心对称图形的个数是（）
| A．2 | B．3 | C．4 | D．5 |
7．如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC等于（ ）
| A．3 cm | B．4cm | C．5cm | D．6cm |
8．如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（ ）
| A．1cm | B．2cm | C．3cm | D．4cm |
9．遂宁市某生态示范园，计划种植一批核桃，原计划总产量达36万千克，为了满足市场需求，现决定改良核桃品种，改良后平均每亩产量是原计划的1.5倍，总产量比原计划增加了9万千克，种植亩数减少了20亩，则原计划和改良后平均每亩产量各是多少万千克？设原计划每亩平均产量为x万千克，则改良后平均每亩产量为1.5x万千克，根据题意列方程为( )
A． － ＝20 | B．－ ＝20 | C．－＝20 | D．＋＝20 |
10．二次函数
（
）的图象如图所示，下列结论：①
；②
；③
；④
；⑤
，其中正确的个数是（ ）
（）的图象如图所示，下列结论：①；②；③；④；⑤，其中正确的个数是（ ）| A．2 | B．3 | C．4 | D．5 |
11．把96000用科学记数法表示为_______________ ．
12．一个n边形的内角和为1080°，则n= ．
13．某射击运动员在一次射击训练中，共射击了6次，所得成绩（单位：环）为：6、8、7、7、8、9，这组数据的中位数是_____ ．
14．在半径为5cm的⊙O中，45°的圆心角所对的弧长为 cm．
15．下列命题：①对角线互相垂直的四边形是菱形；
②点G是△ABC的重心，若中线AD=6，则AG=3；
③若直线
经过第一、二、四象限，则k＜0，b＞0；
④定义新运算：a*b=
，若（2x）*（x﹣3）=0，则x=1或9；
⑤抛物线
的顶点坐标是（1，1）．
其中是真命题的有 （只填序号）
②点G是△ABC的重心，若中线AD=6，则AG=3；
③若直线
经过第一、二、四象限，则k＜0，b＞0；④定义新运算：a*b=
，若（2x）*（x﹣3）=0，则x=1或9；⑤抛物线
的顶点坐标是（1，1）．其中是真命题的有 （只填序号）
16．计算：
．
．17．解不等式组
并将解集在数轴上表示出来．
并将解集在数轴上表示出来．
18．先化简，再求值：
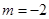，其中
．
，其中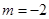
．19．如图，在平行四边形ABCD中，点E、F在对角线BD上，且BE＝DF，
(1)求证：AE＝CF；
(2)求证：四边形AECF是平行四边形．
(1)求证：AE＝CF；
(2)求证：四边形AECF是平行四边形．
20．一数学兴趣小组为了测量河对岸树AB的高，在河岸边选择一点C，从C处测得树梢A的仰角为45°，沿BC方向后退10米到点D，再次测得A的仰角为30°，求树高．（结果精确到0.1米，参考数据：
≈1.414，
≈1.732）
≈1.414，
≈1.732）
21．阅读下列材料，并用相关的思想方法解决问题．
计算：（1﹣
﹣
﹣
）×（++
）﹣（1﹣﹣﹣
）×（++）．
令++=t，则原式=（1﹣t）（t+
）﹣（1﹣t﹣）t=t+﹣t2﹣t﹣
t+t2=，
问题：
（1）计算：（1﹣﹣﹣
）×（++
）﹣（1﹣﹣﹣
）×（++
）；
（2）解方程（x2+5x+1）（x2+5x+7）=7．
计算：（1﹣
﹣
﹣
）×（++
）﹣（1﹣﹣﹣
）×（++）．令
++=t，则原式=（1﹣t）（t+
）﹣（1﹣t﹣）t=t+﹣t2﹣t﹣
t+t2=，问题：
（1）计算：（1﹣
﹣﹣
）×（++
）﹣（1﹣﹣﹣
）×（++
）；（2）解方程（x2+5x+1）（x2+5x+7）=7．
22．（10分）交通指数是交通拥堵指数的简称，是综合反映道路畅通或拥堵的概念．其指数在100以内为畅通，200以上为严重拥堵，从某市交通指挥中心选取了5月1日至14日的交通状况，依据交通指数数据绘制的折线统计图如图所示，某人随机选取了5月1日至14日的某一天到达该市．
（1）请结合折线图分别找出交通为畅通和严重拥堵的天数；
（2）求此人到达当天的交通为严重拥堵的概率；
（3）由图判断从哪天开始连续三天的交通指数方差最大？（直接判断，不要求计算）
（1）请结合折线图分别找出交通为畅通和严重拥堵的天数；
（2）求此人到达当天的交通为严重拥堵的概率；
（3）由图判断从哪天开始连续三天的交通指数方差最大？（直接判断，不要求计算）
23．如图，一次函数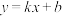
与反比例函数
的图象交于A（1，4），B（4，n）两点．
（1）求反比例函数的解析式；
（2）求一次函数的解析式；
（3）点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小．
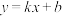与反比例函数
的图象交于A（1，4），B（4，n）两点．
（1）求反比例函数的解析式；
（2）求一次函数的解析式；
（3）点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小．
24．如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．
（1）求证：∠ADC=∠ABD；
（2）求证：AD2=AM•AB；
（3）若AM=
，sin∠ABD=
，求线段BN的长．
（1）求证：∠ADC=∠ABD；
（2）求证：AD2=AM•AB；
（3）若AM=
，sin∠ABD=，求线段BN的长．25．如图，已知抛物线
经过A（﹣2，0），B（4，0），C（0，3）三点．
（1）求该抛物线的解析式；
（2）在y轴上是否存在点M，使△ACM为等腰三角形？若存在，请直接写出所有满足要求的点M的坐标；若不存在，请说明理由；
（3）若点P（t，0）为线段AB上一动点（不与A，B重合），过P作y轴的平行线，记该直线右侧与△ABC围成的图形面积为S，试确定S与t的函数关系式．
经过A（﹣2，0），B（4，0），C（0，3）三点．
（1）求该抛物线的解析式；
（2）在y轴上是否存在点M，使△ACM为等腰三角形？若存在，请直接写出所有满足要求的点M的坐标；若不存在，请说明理由；
（3）若点P（t，0）为线段AB上一动点（不与A，B重合），过P作y轴的平行线，记该直线右侧与△ABC围成的图形面积为S，试确定S与t的函数关系式．
