搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．下列各数比﹣3小的数是( )
| A．0 | B．1 | C．﹣4 | D．﹣1 |
2．下列运算正确的是（）
A． | B． | C． | D． |
3．如图所示的几何体的主视图是（ ）
A． | B． | C． | D． |
4．已知一粒米的质量是0.000021千克，这个数字用科学记数法表示（ ）
A． 千克 | B． 千克 | C． 千克 | D． 千克 |
5．从下列四张卡片中任取一张，卡片上的图形是中心对称图形的概率是【 】
| A．0 | B． | C． | D． |
6．将不等式组
的解集在数轴上表示出来，正确的是（）
的解集在数轴上表示出来，正确的是（）A． | B． |
C． | D． |
7．如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=53°，则∠BCE的度数为【 】
| A．53° | B．37° | C．47° | D．123° |
8．某校开展“节约每一滴水”活动，为了了解开展活动一个月以来节约用水的情况，从八年级的400名同学中选取20名同学统计了各自家庭一个月约节水情况．见表：
请你估计这400名同学的家庭一个月节约用水的总量大约是（ ）
| 节水量/m3 | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
| 家庭数/个 | 2 | 4 | 6 | 7 | 1 |
请你估计这400名同学的家庭一个月节约用水的总量大约是（ ）
| A．130m3 | B．135m3 | C．6.5m3 | D．260m3 |
9．如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（ ）．
| A．3 | B．3.5 | C．2.5 | D．2.8 |
10．二次函数
的图象如图，若一元二次方程
有实数根，则
的最大值为( )
的图象如图，若一元二次方程
有实数根，则
的最大值为( )
A． | B．3 | C． | D．9 |
11．如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是【 】
| A．CM=DM | B． | C．∠ACD=∠ADC | D．OM=MD |
12．将抛物线
向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）
向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）A． | B． | C． | D． |
13．如图，为测量某物体AB的高度，在D点测得A点的仰角为30°，朝物体AB方向前进20米，到达点C，再次测得点A的仰角为60°，则物体AB的高度为（ ）
A．10 米 | B．10米 | C．20米 | D． 米 |
14．如图，菱形OABC的顶点O在坐标原点，顶点A在x轴上，∠B=120°，OA=2，将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为（）
A．（ ， ） | B．（，） | C．（，） | D．（ ， ） |
15．一个不透明的布袋中有分别标着数字1，2，3，4的四个乒乓球，现从袋中随机摸出两个乒乓球，则这两个乒乓球上的数字之和大于5的概率为（ ）
A． | B． | C． | D． |
16．二次函数
的图象如图，则一次函数
的图象经过【 】
的图象如图，则一次函数的图象经过【 】| A．第一、二、三象限 | B．第一、二、四象限 | C．第二、三、四象限 | D．第一、三、四象限 |
17．如图，将矩形纸片ABCD沿EF折叠，使点B与CD的中点重合，若AB=2，BC=3，则△FCB′与△B′DG的面积之比为【 】
| A．9：4 | B．3：2 | C．4：3 | D．16：9 |
18．如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠ABC=120°，OC=3，则
的长为（）
的长为（）
| A．π | B．2π | C．3π | D．5π |
19．设A
，B
，C
是抛物线
上的三点，则
，
，
的大小关系为（ ）
，B，C是抛物线上的三点，则，，的大小关系为（ ）A． | B． | C． | D． |
20．如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5，CD=3，则EF的长是【 】
| A．4 | B．3 | C．2 | D．1 |
21．分解因式：
=______ ；
=22．化简：
=_________ ．
=23．如图，在半径为5的⊙O中，弦AB=6，点C是优弧
上一点（不与A，B重合），则cosC的值为________ ．
上一点（不与A，B重合），则cosC的值为
24．如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第2012个点的横坐标为________ ．
25．如图，一次函数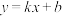
的图象与坐标轴分别交于A，B两点，与反比例函数
的图象在第二象限的交点为C，CD⊥
轴，垂足为D，若OB=2，OD=4，△AOB的面积为1．
（1）求一次函数与反比例函数的解析式；
（2）直接写出当
时，
的解集．
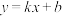的图象与坐标轴分别交于A，B两点，与反比例函数
的图象在第二象限的交点为C，CD⊥
轴，垂足为D，若OB=2，OD=4，△AOB的面积为1．（1）求一次函数与反比例函数的解析式；
（2）直接写出当
时，
的解集．
26．如图，在△ABC中，∠ABC=45°，CD⊥AB，BE⊥AC，垂足分别为D，E，F为BC中点，BE与DF，DC分别交于点G，H，∠ABE=∠CBE．
（1）线段BH与AC相等吗？若相等给予证明，若不相等请说明理由；
（2）求证：BG2﹣GE2=EA2．
（1）线段BH与AC相等吗？若相等给予证明，若不相等请说明理由；
（2）求证：BG2﹣GE2=EA2．
27．一项工程，甲，乙两公司合做，12天可以完成，共需付施工费102000元；如果甲，乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元．
（1）甲，乙两公司单独完成此项工程，各需多少天？
（2）若让一个公司单独完成这项工程，哪个公司的施工费较少？
（1）甲，乙两公司单独完成此项工程，各需多少天？
（2）若让一个公司单独完成这项工程，哪个公司的施工费较少？
28．如图，E是矩形ABCD的边BC上一点，EF⊥AE，EF分别交AC、CD于点M、F，BG⊥AC，垂足为G，BG交AE于点H．
（1）求证：△ABE∽△ECF；
（2）找出与△ABH相似的三角形，并证明；
（3）若E是BC中点，BC=2AB，AB=2，求EM的长．
（1）求证：△ABE∽△ECF；
（2）找出与△ABH相似的三角形，并证明；
（3）若E是BC中点，BC=2AB，AB=2，求EM的长．
29．如图，半径为2的⊙C与x轴的正半轴交于点A，与y轴的正半轴交于点B，点C的坐标为（1，0）．若抛物线
过A、B两点．
（1）求抛物线的解析式；
（2）在抛物线上是否存在点P，使得∠PBO=∠POB？若存在，求出点P的坐标；若不存在说明理由；
（3）若点M是抛物线（在第一象限内的部分）上一点，△MAB的面积为S，求S的最大（小）值．
过A、B两点．（1）求抛物线的解析式；
（2）在抛物线上是否存在点P，使得∠PBO=∠POB？若存在，求出点P的坐标；若不存在说明理由；
（3）若点M是抛物线（在第一象限内的部分）上一点，△MAB的面积为S，求S的最大（小）值．
