搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．-2的绝对值是（ ）
| A．2 | B． | C． | D． |
2．下列运算的结果为a6的是
A． | B． | C． | D． |
3．如图是由六个棱长为1的正方体组成的几何体，其俯视图的面积是（）
| A．3 | B．4 | C．5 | D．6 |
4．如图，将∠AOB放置在5×5的正方形网格中，则tan∠AOB的值是
A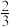． | B． | C． | D． |
5．下列选项中，能够反映一组数据离散程度的统计量是（）
| A．平均数 | B．中位数 | C．众数 | D．方差 |
6．方程
的解是
的解是| A．x=﹣1 | B．x=0 | C．x=1 | D．x=2 |
7．下列三个函数：①y=x+1；②
；③
．其图象既是轴对称图形，又是中心对称图形的个数有（ ）
；③．其图象既是轴对称图形，又是中心对称图形的个数有（ ）| A．0 | B．1 | C．2 | D．3 |
8．在等腰△ABC中，∠ACB=90°，且AC=1．过点C作直线l∥AB，P为直线l上一点，且AP=AB．则点P到BC所在直线的距离是
A．1
B．1或
C．1或
D．或
A．1
B．1或
C．1或
D．
或9．如图，数轴所表示的不等式的解集是_____ ．
10．已知⊙O1与⊙O2相切，两圆半径分别为3和5，则圆心距O1O2的值是_____ ．
11．如图，为测量位于一水塘旁的两点A、B间的距离，在地面上确定点O，分别取OA、OB的中点C、D，量得CD=20m，则A、B之间的距离是_____ m．
12．如图，一个平行四边形的活动框架，对角线是两根橡皮筋．若改变框架的形状，则
也随之变化，两条对角线长度也在发生改变．当为_____ 度时，两条对角线长度相等．
也随之变化，两条对角线长度也在发生改变．当为13．计算
的值是 ．
的值是 ．14．已知圆锥的底面周长是10π，其侧面展开后所得扇形的圆心角为90°，则该圆锥的母线长是_____ ．
15．在平面直角坐标系xOy中，已知点A（0，1），B（1，2），点P在x轴上运动，当点P到A、B两点距离之差的绝对值最大时，点P的坐标是_______ ．
16．若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是___ ．
17．如图，AB是半圆O的直径，且AB=8，点C为半圆上的一点．将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是．（结果保留π）
18．在平面直角坐标系xOy中，一次函数
与反比例函数
的图象交点的横坐标为x0．若k＜x0＜k+1，则整数k的值是_____ ．
与反比例函数
的图象交点的横坐标为x0．若k＜x0＜k+1，则整数k的值是19．计算：
．
．20．先化简，再求值：
，其中x=3．
，其中x=3．21．某景区为方便游客参观，在每个景点均设置两条通道，即楼梯和无障碍通道．如图，已知在某景点P处，供游客上下的楼梯倾斜角为30°（即∠PBA=30°），长度为4m（即PB=4m），无障碍通道PA的倾斜角为15°（即∠PAB=15°）．求无障碍通道的长度．（结果精确到0.1m，参考数据：sin15°≈0.21，cos15°≈0.98）
22．某校为了解“阳光体育”活动的开展情况，从全校2000名学生中，随机抽取部分学生进行问卷调查（每名学生只能填写一项自己喜欢的活动项目），并将调查结果绘制成如下两幅不完整的统计图．
根据以上信息，解答下列问题：
（1）被调查的学生共有 人，并补全条形统计图；
（2）在扇形统计图中，m= ，n= ，表示区域C的圆心角为 度；
（3）全校学生中喜欢篮球的人数大约有 ．
根据以上信息，解答下列问题：
（1）被调查的学生共有 人，并补全条形统计图；
（2）在扇形统计图中，m= ，n= ，表示区域C的圆心角为 度；
（3）全校学生中喜欢篮球的人数大约有 ．
23．如图，在平行四边形ABCD中，AD＞AB．
（1）作出∠ABC的平分线（尺规作图，保留作图痕迹，不写作法）；
（2）若（1）中所作的角平分线交AD于点E，AF⊥BE，垂足为点O，交BC于点F，连接EF．求证：四边形ABFE为菱形．
（1）作出∠ABC的平分线（尺规作图，保留作图痕迹，不写作法）；
（2）若（1）中所作的角平分线交AD于点E，AF⊥BE，垂足为点O，交BC于点F，连接EF．求证：四边形ABFE为菱形．
24．妈妈买回6个粽子，其中1个花生馅，2个肉馅，3个枣馅．从外表看，6个粽子完全一样，女儿有事先吃．
（1）若女儿只吃一个粽子，则她吃到肉馅的概率是 ；
（2）若女儿只吃两个粽子，求她吃到的两个都是肉馅的概率．
（1）若女儿只吃一个粽子，则她吃到肉馅的概率是 ；
（2）若女儿只吃两个粽子，求她吃到的两个都是肉馅的概率．
25．某公司有甲种原料260kg，乙种原料270kg，计划用这两种原料生产A、B两种产品共40件．生产每件A种产品需甲种原料8kg，乙种原料5kg，可获利润900元；生产每件B种产品需甲种原料4kg，乙种原料9kg，可获利润1100元．设安排生产A种产品x件．
（1）完成下表
（2）安排生产A、B两种产品的件数有几种方案？试说明理由；
（3）设生产这批40件产品共可获利润y元，将y表示为x的函数，并求出最大利润．
（1）完成下表
| | 甲（kg） | 乙（kg） | 件数（件） |
| A | | 5x | x |
| B | 4（40﹣x） | | 40﹣x |
（3）设生产这批40件产品共可获利润y元，将y表示为x的函数，并求出最大利润．
26．如图，在△ABC中，∠ABC=90°，边AC的垂直平分线交BC于点D，交AC于点E，连接B
A． （1）若∠C=30°，求证：BE是△DEC外接圆的切线； （2）若BE=  ，BD=1，求△DEC外接圆的直径． |
27．如图，在平面直角坐标系xOy中，二次函数
（a，b是常数）的图象与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点
（1）求a和b的值；
（2）求t的取值范围；
（3）若∠PCQ=90°，求t的值．
（a，b是常数）的图象与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点| A．动直线y=t（t为常数）与抛物线交于不同的两点P、Q． |
（1）求a和b的值；
（2）求t的取值范围；
（3）若∠PCQ=90°，求t的值．
28．如图，在梯形ABCD中，AB∥DC，∠B=90°，且AB=10，BC=6，CD=2．点E从点B出发沿BC方向运动，过点E作EF∥AD交边AB于点F．将△BEF沿EF所在的直线折叠得到△GEF，直线FG、EG分别交AD于点M、N，当EG过点D时，点E即停止运动．设BE=x，△GEF与梯形ABCD的重叠部分的面积为y．
（1）证明△AMF是等腰三角形；
（2）当EG过点D时（如图（3）），求x的值；
（3）将y表示成x的函数，并求y的最大值．
（1）证明△AMF是等腰三角形；
（2）当EG过点D时（如图（3）），求x的值；
（3）将y表示成x的函数，并求y的最大值．
