搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．在有理数2，0，﹣1，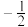
中，最小的是（ ）
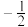中，最小的是（ ）| A．2 | B．0 | C．﹣1 | D． |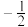
2．2019年6月9日中央电视台新闻报道，端午节期间天猫网共计销售粽子123000000个，将数据123000000用科学记数法表示为（ ）
A．12.3×10 | B．1.23×10 | C．1.23×10 | D．0.123×10 |
3．如图，这是由7个相同的小正方体搭成的几何体，则这个几何体的左视图是（ ）
A． | B． | C． | D． |
4．下列运算正确的是（ ）
A．（﹣a ） ＝﹣a | B．3a•2a＝6a |
| C．﹣a（﹣a+1）＝﹣a+a | D．a+a＝a |
5．如图，某人从点A出发，前进8m后向右转60°，再前进8m后又向右转60°，按照这样的方式一直走下去，当他第一次回到出发点A时，共走了（ ）
| A．24m | B．32m | C．40m | D．48m |
6．如图，AB∥CD，EF与AB，CD分别交于点G，H，∠CHG的平分线HM交AB于点M，若∠EGB＝50°，则∠GMH的度数为（ ）
| A．50° | B．55° | C．60° | D．65° |
7．如图，若一次函数y＝﹣2x+b的图象与两坐标轴分别交于A，B两点，点A的坐标为（0，3），则不等式﹣2x+b＞0的解集为（ ）
A．x＞ | B．x＜ | C．x＞3 | D．x＜3 |
8．如图，正方形ABCD和正方形CGFE的顶点C，D，E在同一条直线上，顶点B，C，G在同一条直线上．O是EG的中点，∠EGC的平分线GH过点D，交BE于点H，连接FH交EG于点M，连接OH．以下四个结论：①GH⊥BE；②△EHM∽△GHF；③
﹣1；④
＝2﹣
，其中正确的结论是（ ）
﹣1；④
＝2﹣
，其中正确的结论是（ ）
| A．①②③ | B．①②④ | C．①③④ | D．②③④ |
9．在函数
中, 自变量
的取值范围是___________ .
中, 自变量的取值范围是10．一个不透明的口袋中有红球和黑球共25个，这些球除颜色外都相同．进行大量的摸球试验（每次摸出1个球）后，发现摸到黑球的频率在0.6附近摆动，据此可以估计黑球为___个．
11．关于x的方程x2+3x+k﹣1＝0有两个相等的实数根，则k的值为___ ．
12．如图，在菱形ABCD中，E，F分别是AD，DC的中点，若BD＝4，EF＝3，则菱形ABCD的周长为__ ．
13．如图，AC是⊙O的直径，B，D是⊙O上的点，若⊙O的半径为3，∠ADB＝30°，则
的长为____．
的长为____．
14．为了美化校园环境，某中学今年春季购买了A，B两种树苗在校园四周栽种，已知A种树苗的单价比B种树苗的单价多10元，用600元购买A种树苗的棵数恰好与用450元购买B种树苗的棵数相同．若设A种树苗的单价为x元，则可列出关于x的方程为___．
15．如图，正方形A0B0C0A1的边长为1，正方形A1B1C1A2的边长为2，正方形A2B2C2A3的边长为4，正方形A3B3C3A4的边长为8……依此规律继续作正方形AnBn∁nAn+1，且点A0，A1，A2，A3，…，An+1在同一条直线上，连接A0C1交A1B1于点D1，连接A1C2交A2B2于点D2，连接A2C3交A3B3于点D3……记四边形A0B0C0D1的面积为S1，四边形A1B1C1D2的面积为S2，四边形A2B2C2D3的面积为S3……四边形An﹣1Bn﹣1Cn﹣1Dn的面积为Sn，则S2019＝_____．
16．如图，在矩形ABCD中，AB＝5，BC＝6，点M，N分别在AD，BC上，且AM＝
AD，BN＝BC，E为直线BC上一动点，连接DE，将△DCE沿DE所在直线翻折得到△DC′E，当点C′恰好落在直线MN上时，CE的长为___ ．
AD，BN＝BC，E为直线BC上一动点，连接DE，将△DCE沿DE所在直线翻折得到△DC′E，当点C′恰好落在直线MN上时，CE的长为
17．先化简，再求值：（
﹣
）÷
，其中x＝3+
．
﹣
）÷
，其中x＝3+
．18．如图，△ABC的三个顶点的坐标分别是A（2，4），B（1，1），C（3，2）．
（1）作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标．
（2）已知△A2B2C2与△ABC关于直线l对称，若点C2的坐标为（﹣2，﹣3），请直接写出直线l的函数解析式．注：点A1，B1，C1及点A2，B2，C2分别是点A，B，C按题中要求变换后对应得到的点．
（1）作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标．
（2）已知△A2B2C2与△ABC关于直线l对称，若点C2的坐标为（﹣2，﹣3），请直接写出直线l的函数解析式．注：点A1，B1，C1及点A2，B2，C2分别是点A，B，C按题中要求变换后对应得到的点．
19．随着我国经济社会的发展，人民对于美好生活的追求越来越高．某社区为了了解家庭对于文化教育的消费情况，随机抽取部分家庭，对每户家庭的文化教育年消费金额进行问卷调查，根据调查结果绘制成如下两幅不完整的统计图表．
请你根据统计图表提供的信息，解答下列问题：
（1）本次被调查的家庭有 户，表中m＝ ；
（2）请说明本次调查数据的中位数落在哪一组？
（3）在扇形统计图中，D组所在扇形的圆心角为多少度？
（4）这个社区有2500户家庭，请你估计年文化教育消费在10000元以上的家庭有多少户？
| 组别 | 家庭年文化教育消费金额x（元） | 户数 |
| A | x≤5000 | 36 |
| B | 5000＜x≤10000 | 27 |
| C | 10000＜x≤15000 | m |
| D | 15000＜x≤20000 | 33 |
| E | x＞20000 | 30 |
（1）本次被调查的家庭有 户，表中m＝ ；
（2）请说明本次调查数据的中位数落在哪一组？
（3）在扇形统计图中，D组所在扇形的圆心角为多少度？
（4）这个社区有2500户家庭，请你估计年文化教育消费在10000元以上的家庭有多少户？
20．妈妈给小红和弟弟买了一本刘慈欣的小说《流浪地球》，姐弟俩都想先睹为快．是小红对弟弟说：我们利用下面中心涂黑的九宫格图案（如图所示）玩一个游戏，规则如下：我从第一行，你从第三行，同时各自任意选取一个方格，涂黑，如果得到的新图案是轴对称图形．我就先读，否则你先读．小红设计的游戏对弟弟是否公平？请用画树状图或列表的方法说明理由．（第一行的小方格从左至右分别用A，B，C表示，第三行的小方格从左至右分别用D，E，F表示）
21．如图，在平面直角坐标系中，一次函数y＝mx+n（m≠0）的图象与y轴交于点C，与反比例函数y＝
（k≠0）的图象交于A，B两点，点A在第一象限，纵坐标为4，点B在第三象限，BM⊥x轴，垂足为点M，BM＝OM＝2．
（1）求反比例函数和一次函数的解析式．
（2）连接OB，MC，求四边形MBOC的面积．
（k≠0）的图象交于A，B两点，点A在第一象限，纵坐标为4，点B在第三象限，BM⊥x轴，垂足为点M，BM＝OM＝2．（1）求反比例函数和一次函数的解析式．
（2）连接OB，MC，求四边形MBOC的面积．
22．如图为某海域示意图，其中灯塔D的正东方向有一岛屿C．一艘快艇以每小时20nmile的速度向正东方向航行，到达A处时得灯塔D在东北方向上，继续航行0.3h，到达B处时测得灯塔D在北偏东30°方向上，同时测得岛屿C恰好在B处的东北方向上，此时快艇与岛屿C的距离是多少？（结果精确到1nmile．参考数据：
≈1.41，≈1.73，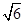
≈2.45）
≈1.41，≈1.73，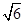
≈2.45）
23．如图，在Rt△ABC中，∠ACB＝90°，D是AC上一点，过B，C，D三点的⊙O交AB于点E，连接ED，EC，点F是线段AE上的一点，连接FD，其中∠FDE＝∠DCE．
（1）求证：DF是⊙O的切线．
（2）若D是AC的中点，∠A＝30°，BC＝4，求DF的长．
（1）求证：DF是⊙O的切线．
（2）若D是AC的中点，∠A＝30°，BC＝4，求DF的长．
24．某商场销售一种商品的进价为每件30元，销售过程中发现月销售量y（件）与销售单价x（元）之间的关系如图所示．
（1）根据图象直接写出y与x之间的函数关系式．
（2）设这种商品月利润为W（元），求W与x之间的函数关系式．
（3）这种商品的销售单价定为多少元时，月利润最大？最大月利润是多少？
（1）根据图象直接写出y与x之间的函数关系式．
（2）设这种商品月利润为W（元），求W与x之间的函数关系式．
（3）这种商品的销售单价定为多少元时，月利润最大？最大月利润是多少？
25．在Rt△ABC中，∠ACB＝90°，D是△ABC内一点，连接AD，BD．在BD左侧作Rt△BDE，使∠BDE＝90°，以AD和DE为邻边作▱ADEF，连接CD，DF．
（1）若AC＝BC，BD＝DE．
①如图1，当B，D，F三点共线时，CD与DF之间的数量关系为 ．
②如图2，当B，D，F三点不共线时，①中的结论是否仍然成立？请说明理由．
（2）若BC＝2AC，BD＝2DE，
，且E，C，F三点共线，求
的值．
（1）若AC＝BC，BD＝DE．
①如图1，当B，D，F三点共线时，CD与DF之间的数量关系为 ．
②如图2，当B，D，F三点不共线时，①中的结论是否仍然成立？请说明理由．
（2）若BC＝2AC，BD＝2DE，
，且E，C，F三点共线，求
的值．26．在平面直角坐标系中，过点A（3，4）的抛物线y＝ax2+bx+4与x轴交于点B（﹣1，0），与y轴交于点C，过点A作AD⊥x轴于点D．
（1）求抛物线的解析式．
（2）如图1，点P是直线AB上方抛物线上的一个动点，连接PD交AB于点Q，连接AP，当S△AQD＝2S△APQ时，求点P的坐标．
（3）如图2，G是线段OC上一个动点，连接DG，过点G作GM⊥DG交AC于点M，过点M作射线MN，使∠NMG＝60°，交射线GD于点N；过点G作GH⊥MN，垂足为点H，连接BH．请直接写出线段BH的最小值．
（1）求抛物线的解析式．
（2）如图1，点P是直线AB上方抛物线上的一个动点，连接PD交AB于点Q，连接AP，当S△AQD＝2S△APQ时，求点P的坐标．
（3）如图2，G是线段OC上一个动点，连接DG，过点G作GM⊥DG交AC于点M，过点M作射线MN，使∠NMG＝60°，交射线GD于点N；过点G作GH⊥MN，垂足为点H，连接BH．请直接写出线段BH的最小值．
