全一卷
1.如图,是北京奥运会自行车比赛项目标志,则图中两轮所在圆的位置关系是()


| A.内含 | B.相交 | C.相切 | D.外离 |
2.化简 的结果是【 】
| A.3 | B.-3 | C.±3 | D.9 |
3.如果2是方程 的一个根,那么c的值是( )
的一个根,那么c的值是( )
 的一个根,那么c的值是( )
的一个根,那么c的值是( )A. | B.-4 | C.2 | D.-2 |
4.下列成语所描述的事件是必然发生的是( )
| A.水中捞月 | B.拔苗助长 | C.守株待兔 | D.瓮中捉鳖 |
5.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB="20,CD=16," 那么线段OE的长为( )


| A.10 | B.8 | C.6 | D.4 |
6.抛物线 的顶点坐标是 【 】
的顶点坐标是 【 】
 的顶点坐标是 【 】
的顶点坐标是 【 】| A.(-2,3) | B.(2,3) | C.(-2,-3) | D.(2,-3) |
7.观察下列银行标志,从图案看是中心对称图形的有( )个








| A.1个 | B.2个 | C.3个 | D.4个 |
8.二次函数 的图象与
的图象与 轴有交点,则
轴有交点,则 的取值范围是【 】
的取值范围是【 】
 的图象与
的图象与 轴有交点,则
轴有交点,则 的取值范围是【 】
的取值范围是【 】A. | B. | C. | D. |
9.某校九年级(1)班50名学生中有20名团员,他们都积极报名参加学校开展的“文明劝导活动”.根据要求,该班从团员中随机抽取1名参加,则该班团员京京被抽到的概率是 ( )
A. | B. | C. | D. |
10.在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是【 】


A. | B.1 | C.2 | D. |
11.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )


| A.R=2r; | B. ; ; | C.R=3r; | D.R=4r. |
12.已知反比例函数 的图象如下右图所示,则二次函数
的图象如下右图所示,则二次函数 的图象大致为()
的图象大致为()

 的图象如下右图所示,则二次函数
的图象如下右图所示,则二次函数 的图象大致为()
的图象大致为()
A. | B. | C. | D. |
13.如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上一点,且∠EPF=40°,则图中阴影部分的面积是【 】


A. | B. | C. | D. |
14.点(4,-3)关于原点对称的点的坐标是 ____ .
15.⊙O的半径为3cm,点M是⊙O外一点,OM=4cm,则以M为圆心且与⊙O相切的圆的半径是__ cm.
16.将抛物线 向下平移3个单位,再向左平移4个单位得到抛物线
向下平移3个单位,再向左平移4个单位得到抛物线 ,则原抛物线的顶点坐标是
,则原抛物线的顶点坐标是__________
 向下平移3个单位,再向左平移4个单位得到抛物线
向下平移3个单位,再向左平移4个单位得到抛物线 ,则原抛物线的顶点坐标是
,则原抛物线的顶点坐标是17.某商店经营一种水产品,成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,销售单价定为__________ 元时,获得的利润最多.
18.阅读材料:设一元二次方程 的两根为
的两根为 ,
, ,则两根与方程系数之间有如下关系
,则两根与方程系数之间有如下关系 ,
, 根据该材料填空:已知
根据该材料填空:已知 ,
, 是方程
是方程 的两实数根,则
的两实数根,则 的值为____ __
的值为____ __
 的两根为
的两根为 ,
, ,则两根与方程系数之间有如下关系
,则两根与方程系数之间有如下关系 ,
, 根据该材料填空:已知
根据该材料填空:已知 ,
, 是方程
是方程 的两实数根,则
的两实数根,则 的值为____ __
的值为____ __19.计算:

20.解方程:

21.如上图,在 正方形网格中,每个小正方形的边长均为1个单位.
正方形网格中,每个小正方形的边长均为1个单位.
(1)作 关于点P的对称图形
关于点P的对称图形 .
.
(2)再把 ,绕着
,绕着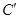 逆顺时针旋转
逆顺时针旋转 ,得到
,得到 ,请你画出
,请你画出 和
和 (不要求写画法).
(不要求写画法).
 正方形网格中,每个小正方形的边长均为1个单位.
正方形网格中,每个小正方形的边长均为1个单位.(1)作
 关于点P的对称图形
关于点P的对称图形 .
.(2)再把
 ,绕着
,绕着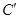 逆顺时针旋转
逆顺时针旋转 ,得到
,得到 ,请你画出
,请你画出 和
和 (不要求写画法).
(不要求写画法).
22.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5cm,求铁环的半径.

23.已知,如图,直线 经过
经过 和
和 两点,它与抛物线
两点,它与抛物线 在第一象限内相交于点P,又知
在第一象限内相交于点P,又知 的面积为4,求
的面积为4,求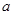 的值.
的值.
 经过
经过 和
和 两点,它与抛物线
两点,它与抛物线 在第一象限内相交于点P,又知
在第一象限内相交于点P,又知 的面积为4,求
的面积为4,求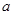 的值.
的值.
24.汉字是世界上最古老的文字之一,字形结构体现人类追求均衡对称、和谐稳定的天性.如图,三个汉字可以看成是轴对称图形.

(1)请在方框中再写出2个类似轴对称图形的汉字;

(2)小敏和小慧利用“土”、“口”、“木”三个汉字设计一个游戏,规则如下:将这三个汉字分别写在背面都相同的三张卡片上,背面朝上洗匀后抽出一张,放回洗匀后再抽出一张,若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”)小敏获胜,否则小慧获胜.你认为这个游戏对谁有利?请用列表或画树状图的方法进行分析并写出构成的汉字进行说明.

(1)请在方框中再写出2个类似轴对称图形的汉字;

(2)小敏和小慧利用“土”、“口”、“木”三个汉字设计一个游戏,规则如下:将这三个汉字分别写在背面都相同的三张卡片上,背面朝上洗匀后抽出一张,放回洗匀后再抽出一张,若两次抽出的汉字能构成上下结构的汉字(如“土”“土”构成“圭”)小敏获胜,否则小慧获胜.你认为这个游戏对谁有利?请用列表或画树状图的方法进行分析并写出构成的汉字进行说明.
25.已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.

求证:(1)△ABC是等边三角形;
(2) .
.

求证:(1)△ABC是等边三角形;
(2)
 .
.26.如图,足球场上守门员在 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出(
处飞出( 在
在 轴上),运动员乙在距
轴上),运动员乙在距 点6米的
点6米的 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.

(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点 距守门员多少米?(取
距守门员多少米?(取 )
)
(3)运动员乙要抢到第二个落点 ,他应再向前跑多少米?
,他应再向前跑多少米?
(取 )
)
 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出(
处飞出( 在
在 轴上),运动员乙在距
轴上),运动员乙在距 点6米的
点6米的 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点
 距守门员多少米?(取
距守门员多少米?(取 )
)(3)运动员乙要抢到第二个落点
 ,他应再向前跑多少米?
,他应再向前跑多少米?(取
 )
)27.已知两个关于 的二次函数
的二次函数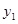 与
与 ,当
,当 时,
时, ;且二次函数
;且二次函数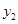 的图象的对称轴是直线
的图象的对称轴是直线 .
.
(1)求 的值;
的值;
(2)求函数 的表达式;
的表达式;
(3)在同一直角坐标系内,问函数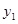 的图象与
的图象与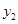 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由.
 的二次函数
的二次函数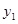 与
与 ,当
,当 时,
时, ;且二次函数
;且二次函数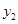 的图象的对称轴是直线
的图象的对称轴是直线 .
.(1)求
 的值;
的值;(2)求函数
 的表达式;
的表达式;(3)在同一直角坐标系内,问函数
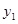 的图象与
的图象与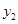 的图象是否有交点?请说明理由.
的图象是否有交点?请说明理由. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
