搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．－5的倒数是
A． | B．5 | C．－ | D．－5 |
2．乐山大佛景区2013年5月份某周的最高气温（单位：℃）分别为：29，31，23，26，29，29．这组数据的极差为（ ）
| A．29 | B．28 | C．8 | D．6 |
3．如图，已知直线a∥b，∠1=1310，则∠2等于（）
| A．390 | B．410 | C．490 | D．590 |
4．若
，则下列不等式变形错误的是【 】
，则下列不等式变形错误的是【 】A． | B． | C． | D． |
5．如图，点E是
的边CD的中点，AD、BE的延长线相交于点F，DF=3，DE=2，则的周长为( )
的边CD的中点，AD、BE的延长线相交于点F，DF=3，DE=2，则的周长为( )| A．5 | B．7 | C．10 | D．14 |
6．如图，在平面直角坐标系中，P是第一象限内的点，其坐标是(3，m)，且OP与x轴正半轴的夹角α的正切值是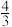
，则sinα的值是( )
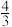，则sinα的值是( )
A． | B． | C． | D． |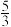
7．甲、乙两人同时分别从A，B两地沿同一条公路骑自行车到C地．已知A，C两地间的距离为110千米，B，C两地间的距离为100千米．甲骑自行车的平均速度比乙快2千米/时．结果两人同时到达C地．求两人的平均速度，为解决此问题，设乙骑自行车的平均速度为x千米/时．由题意列出方程．其中正确的是（ ）
A． | B． | C． | D． |
8．一个立体图形的三视图如图所示，根据图中数据求得这个立体图形的的表面积为（ ）
A． | B． | C． | D． |
9．如图，圆心在y轴的负半轴上，半径为5的⊙B与y轴的正半轴交于点A（0，1）。过点P（0，－7）的直线l与⊙B相交于C、D两点，则弦CD长的所有可能的整数值有（ ）条.
A．1 B．2 C．3 D．4
A．1 B．2 C．3 D．4
10．如图，已知第一象限内的点A在反比例函数y=
的图象上，第二象限内的点B在反比例函数y=
的图象上，且OA⊥OB，cosA=
，则k的值为（）
的图象上，第二象限内的点B在反比例函数y=
的图象上，且OA⊥OB，cosA=
，则k的值为（）
| A．﹣3 | B．﹣4 | C．﹣ | D．﹣2 |
11．如果规定向东为正，那么向西即为负．汽车向东行驶3千米记作
千米，向西行驶2千米应记作____ ．
千米，向西行驶2千米应记作12．在一个布口袋里装有白、红、黑三种颜色的小球．它们除颜色外没有任何其他区别，其中白球5只、红球3只、黑球1只．袋中的球已经搅匀，闭上眼睛随机地从装中取出1只球，取出红球的概率是____ ．
13．把多项式分解因式：
．
．14．如图，在四边形ABCD中，∠A=450，直线l与边AB、AD分别相交于点M、N．则∠1 ＋∠2 = ．
15．如图，小方格都是边长为1 的正方形．则以格点为圆心，半径为1和2的两种弧围成的“叶状”阴影图案的面积为____ ．
16．对非负实数x“四舍五入”到个位的值记为<x>，即当n为非负整数时，若
，则<x>＝n，如<0.46>=0，<3.67>=4。给出下列关于<x>的结论：
①<1.493>=1；
②<2x>=2<x>；
③若
，则实数x的取值范围是
；
④当x≥0，m为非负整数时，有
；
⑤
。
其中，正确的结论有 （填写所有正确的序号）。
，则<x>＝n，如<0.46>=0，<3.67>=4。给出下列关于<x>的结论：①<1.493>=1；
②<2x>=2<x>；
③若
，则实数x的取值范围是
；④当x≥0，m为非负整数时，有
；⑤
。其中，正确的结论有 （填写所有正确的序号）。
17．化简：
．
．18．如图，已知线段AB．
（1）用尺规作图的方法作出线段AB的垂直平分线l（保留作图痕迹，不要求写出作法）；
（2）在（1）中所作的直线l上任意取两点M、N（线段AB的上方），连接AM、AN．BM、BN．
求证：∠MAN=∠MBN．
（1）用尺规作图的方法作出线段AB的垂直平分线l（保留作图痕迹，不要求写出作法）；
（2）在（1）中所作的直线l上任意取两点M、N（线段AB的上方），连接AM、AN．BM、BN．
求证：∠MAN=∠MBN．
19．化简并求值：
，其中x、y满足
，其中x、y满足20．中学生带手机上学的现象越来越受到社会的关注，为此，某记者随机调查了某城区若干名学生家长对这种现象的态度（态度分为：A：无所谓；B：基本赞成；C：赞成；D：反对），并将调查结果绘制成频数折线图1和统计图2（不完整）．请根据图中提供的信息，解答下列问题：
（1）此次抽样检查中，共调查了 名学生家长；
（2）将图1补充完整；
（3）根据抽样检查的结果，请你估计该市城区6000名中学生家长中有多少名家长持反对态度？
（1）此次抽样检查中，共调查了 名学生家长；
（2）将图1补充完整；
（3）根据抽样检查的结果，请你估计该市城区6000名中学生家长中有多少名家长持反对态度？
21．如图，山顶有一铁塔AB的高度为20米，为测量山的高度BC，在山脚点D处测得塔顶A和塔基B的仰角分别为60°和45°．求山的高度B
| A．（结果保留根号） |
22．如图，AB是⊙O的直径，经过圆上点D的直线CD恰∠ADC=∠B。
（1）求证：直线CD是⊙O的的切线；
（2）过点A作直线AB的垂线交BD的延长线于点E，且AB=
，BD=2，求线段AE的长。
（1）求证：直线CD是⊙O的的切线；
（2）过点A作直线AB的垂线交BD的延长线于点E，且AB=
，BD=2，求线段AE的长。23．已知关于x、y的方程组
的解满足不等式组
．求满足条件的m的整数值．
的解满足不等式组
．求满足条件的m的整数值．24．已知关于x的一元二次方程
（1）求证：方程有两个不相等的实数根；
（2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5．当△ABC是等腰三角形时，求k的值
（1）求证：方程有两个不相等的实数根；
（2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5．当△ABC是等腰三角形时，求k的值
25．如图，已知直线
与反比例函数
的图象交于A、B两点，与x 轴、y轴分别相交于C、D两点．
（1）如果点A的横坐标为1，利用函数图象求关于x的不等式
的解集；
（2）是否存在以AB为直径的圆经过点P（1，0）？若存在，求出m的值；若不存在，请说明理由．
与反比例函数
的图象交于A、B两点，与x 轴、y轴分别相交于C、D两点．
（1）如果点A的横坐标为1，利用函数图象求关于x的不等式
的解集；（2）是否存在以AB为直径的圆经过点P（1，0）？若存在，求出m的值；若不存在，请说明理由．
26．阅读下列材料：
如图1，在梯形ABCD中，AD∥BC，点M、N分别在边AB、BC上，且MN∥AD，记AD=a，BC=b，若
，则有结论：
．
请根据以上结论，解答下列问题：
如图2，3，BE、CF是△ABC的两条角平分线，过EF上一点P分别作△ABC三边的垂线段PP1、PP2、PP3，交BC于点P1，交AB于点P2，交AC于点P3．
（1）若点P为线段EF的中点，求证：PP1=PP2＋PP3；
（2）若点P在线段EF上任意位置时，试探究PP1、PP2、PP3的数量关系，给出证明．
如图1，在梯形ABCD中，AD∥BC，点M、N分别在边AB、BC上，且MN∥AD，记AD=a，BC=b，若
，则有结论：
．
请根据以上结论，解答下列问题：
如图2，3，BE、CF是△ABC的两条角平分线，过EF上一点P分别作△ABC三边的垂线段PP1、PP2、PP3，交BC于点P1，交AB于点P2，交AC于点P3．
（1）若点P为线段EF的中点，求证：PP1=PP2＋PP3；
（2）若点P在线段EF上任意位置时，试探究PP1、PP2、PP3的数量关系，给出证明．
27．如图1，已知抛物线C经过原点，对称轴
与抛物线相交于第三象限的点M，与x轴相交于点N，且
．
（1）求抛物线C的解析式；
（2）将抛物线C绕原点O旋转1800得到抛物线
，抛物线与x轴的另一交点为A，B为抛物线上横坐标为2的点．
①若P为线段AB上一动点，PD⊥y轴于点D，求△APD面积的最大值；
②过线段OA上的两点E、F分别作x轴的垂线，交折线O－B－A于E1、F1，再分别以线段EE1、FF1为边作如图2所示的等边△AE1E2、等边△AF1F2，点E以每秒1个长度单位的速度从点O向点A运动，点F以每秒1个长度单位的速度从点A向点O运动，当△AE1E2有一边与△AF1F2的某一边在同一直线上时，求时间t的值．
与抛物线相交于第三象限的点M，与x轴相交于点N，且
．
（1）求抛物线C的解析式；
（2）将抛物线C绕原点O旋转1800得到抛物线
，抛物线与x轴的另一交点为A，B为抛物线上横坐标为2的点．①若P为线段AB上一动点，PD⊥y轴于点D，求△APD面积的最大值；
②过线段OA上的两点E、F分别作x轴的垂线，交折线O－B－A于E1、F1，再分别以线段EE1、FF1为边作如图2所示的等边△AE1E2、等边△AF1F2，点E以每秒1个长度单位的速度从点O向点A运动，点F以每秒1个长度单位的速度从点A向点O运动，当△AE1E2有一边与△AF1F2的某一边在同一直线上时，求时间t的值．
