全一卷
1.﹣3的相反数是( )
A. | B. | C. | D. |
2.下列运算正确的是( )
| A.3a+2a=a5 | B.a2·a3=a6 | C.(a+b)(a-b)=a2-b2 | D.(a+b)2=a2+b2 |
3.如图所示,由三个相同的小正方体组成的立体图形的主视图是( )


A. | B. | C. | D. |
4.为了参加中学生篮球运动会,某校篮球队准备购买10双运动鞋,经统计10双运动鞋的尺码(cm)如下表所示:
则这10双运动鞋的众数和中位数分别为()
| 尺码 | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量(双) | 2 | 4 | 2 | 1 | 1 |
则这10双运动鞋的众数和中位数分别为()
| A.25.5 cm 26 cm | B.26 cm 25.5 cm | C.26 cm 26 cm | D.25.5 cm 25.5 cm |
5.已知两圆半径分别为7,3,圆心距为4,则这两圆的位置关系为()
| A.外离 | B.内切 | C.相交 | D.内含 |
6.已知等腰三角形的其中两边长分别为4,9,则这个等腰三角形的周长是( )
| A.13 | B.17 | C.22 | D.17或22 |
7.已知二次函数 ,当自变量x分别取
,当自变量x分别取 ,3,0时,对应的值分别为
,3,0时,对应的值分别为 ,则
,则 的大小关系正确的是()
的大小关系正确的是()
 ,当自变量x分别取
,当自变量x分别取 ,3,0时,对应的值分别为
,3,0时,对应的值分别为 ,则
,则 的大小关系正确的是()
的大小关系正确的是()A. | B. | C. | D. |
8.已知a、b、c、d都是正实数,且 ,给出下列四个不等式:
,给出下列四个不等式:
① ;②
;② ;③
;③ ;④
;④ .
.
其中不等式正确的是( )
 ,给出下列四个不等式:
,给出下列四个不等式:①
 ;②
;② ;③
;③ ;④
;④ .
.其中不等式正确的是( )
| A.①③ | B.①④ | C.②④ | D.②③ |
9.计算:∣-2∣=______ , =
=_______ , =
=_______ , =
=_______ .
 =
= =
= =
=10.已知点P(-3,1),则点P关于y轴的对称点的坐标是___ ,点P关于原点O的对称点的坐标是_____ .
11.若∠α=60°,则∠α的余角为________ ,cosα的值为_______ .
12.已知扇形的半径为3 cm,圆心角为120°,则此扇形的的弧长是______ cm,扇形的面积是_______ cm2(结果保留π).
13.已知函数 ,则自变量x的取值范围是
,则自变量x的取值范围是______ ;若分式 的值为0,则x=
的值为0,则x=_______ .
 ,则自变量x的取值范围是
,则自变量x的取值范围是 的值为0,则x=
的值为0,则x=14.已知关于x的方程 的一个根是2,则
的一个根是2,则
______ ,另一根为___ .
 的一个根是2,则
的一个根是2,则
15.已知 ,则代数式
,则代数式 的值为
的值为_______ .
 ,则代数式
,则代数式 的值为
的值为16.在平面直角坐标系xOy中,已知点P(3,0),⊙P是以点P为圆心,2为半径的圆.若一次函数 的图象过点A(-1,0)且与⊙P相切,则
的图象过点A(-1,0)且与⊙P相切,则 的值为
的值为______ .
 的图象过点A(-1,0)且与⊙P相切,则
的图象过点A(-1,0)且与⊙P相切,则 的值为
的值为17.如图,已知反比例函数 和
和 .点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、O
.点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、O
 和
和 .点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、O
.点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OA.若△BOC的面积为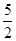 ,AC:AB=2:3,则 ,AC:AB=2:3,则 = ▲ , = ▲ , = ▲ . = ▲ . |
18.化简(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.19.解方程组和不等式组:
(1)解方程组: ;(2)解不等式组:
;(2)解不等式组: .
.
(1)解方程组:
 ;(2)解不等式组:
;(2)解不等式组: .
.20.为了迎接党的十八大的召开,某校组织了以“党在我心中”为主题的征文比赛,每位学生只能参加一次比赛,比赛成绩分A、B、C、D四个等级,随机抽取该校部分学生的征文比赛成绩进行分析,并绘制了如下的统计图表:

根据表中的信息,解决下列问题:
(1)本次抽查的学生共有 ▲ 名;
(2)表中x、y和m所表示的数分别为x= ▲ ,y= ▲ ,m= ▲ ;
(3)补全条形统计图.
| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 占抽查学生总数的百分比 | 30% | 50% | 15% | m |

根据表中的信息,解决下列问题:
(1)本次抽查的学生共有 ▲ 名;
(2)表中x、y和m所表示的数分别为x= ▲ ,y= ▲ ,m= ▲ ;
(3)补全条形统计图.
21.在一个不透明的口袋里装有白、红、黑三种颜色的小球,其中白球2只,红球1只,黑球1只,它们除了颜色之外没有其它区别.从袋中随机地摸出1只球,记录下颜色后放回搅匀,再第二个球并记录颜色.求两次都摸出白球的概率.
22.如图,在△ABC中,AB=AC,AD平分∠BAC,求证:∠DBC=∠DCB.


23.如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂直平分线分别与AD、BC相交于点E、F,连接AF.
求证:AE=AF.
求证:AE=AF.

24.如图,在平面直角坐标系 中,已知△ABC和△DEF的顶点分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
中,已知△ABC和△DEF的顶点分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
按下列要求画图:以点O为位似中心,将△ABC向y轴左侧按比例尺2:1放大得△ABC的位似图形△A1B1C1,并解决下列问题:
(1)顶点A1的坐标为 ,B1的坐标为 ,C1的坐标为 ;
(2)请你利用旋转、平移两种变换,使△A1B1C1通过变换后得到△A2B2C2,且△A2B2C2恰与△DEF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.

 中,已知△ABC和△DEF的顶点分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
中,已知△ABC和△DEF的顶点分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).按下列要求画图:以点O为位似中心,将△ABC向y轴左侧按比例尺2:1放大得△ABC的位似图形△A1B1C1,并解决下列问题:
(1)顶点A1的坐标为 ,B1的坐标为 ,C1的坐标为 ;
(2)请你利用旋转、平移两种变换,使△A1B1C1通过变换后得到△A2B2C2,且△A2B2C2恰与△DEF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.

25.某商场购进一批L型服装(数量足够多),进价为40元/件,以60元/件销售,每天销售20件。根据市场调研,若每件每降1元,则每天销售数量比原来多3件。现商场决定对L型服装开展降价促销活动,每件降价x元(x为正整数)。在促销期间,商场要想每天获得最大销售利润,每件降价多少元?每天最大销售毛利润为多少?(注:每件服装销售毛利润指每件服装的销售价与进货价的差)
26.平面上两条直线AB、CD相交于点O,且∠BOD=1500(如图),现按如下要求规定此平面上点的“距离坐标”:
(1)点O的“距离坐标”为(0,0);
(2)在直线CD上,且到直线AB的距离为p(p>0)的点的“距离坐标”为(p,0);在直线AB上,且到直线CD的距离为q(q>0)的点的“距离坐标”为(0,q);
(3)到直线AB、CD的距离分别为p、q(p>0,q>0)的点的“距离坐标”为(p,q).
设M为此平面上的点,其“距离坐标”为(m,n),根据上述对点的“距离坐标”的规定,解决下列问题:
(1)画出图形(保留画图痕迹):
①满足m=1且n=0的点的集合;
②满足m=n的点的集合;
(2)若点M在过点O且与直线CD垂直的直线l上,求m与n所满足的关系式.
(说明:图中OI长为一个单位长)
(1)点O的“距离坐标”为(0,0);
(2)在直线CD上,且到直线AB的距离为p(p>0)的点的“距离坐标”为(p,0);在直线AB上,且到直线CD的距离为q(q>0)的点的“距离坐标”为(0,q);
(3)到直线AB、CD的距离分别为p、q(p>0,q>0)的点的“距离坐标”为(p,q).
设M为此平面上的点,其“距离坐标”为(m,n),根据上述对点的“距离坐标”的规定,解决下列问题:
(1)画出图形(保留画图痕迹):
①满足m=1且n=0的点的集合;
②满足m=n的点的集合;
(2)若点M在过点O且与直线CD垂直的直线l上,求m与n所满足的关系式.
(说明:图中OI长为一个单位长)

27.已知,在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D两点).连接PM,过点P作PM的垂线与射线DA相交于点E(如图).设CP=x,DE=y.
(1)写出y与x之间的函数关系式 ▲ ;
(2)若点E与点A重合,则x的值为 ▲ ;
(3)是否存在点P,使得点D关于直线PE的对称点D′落在边AB上?若存在,求x的值;若不存在,请说明理由.
(1)写出y与x之间的函数关系式 ▲ ;
(2)若点E与点A重合,则x的值为 ▲ ;
(3)是否存在点P,使得点D关于直线PE的对称点D′落在边AB上?若存在,求x的值;若不存在,请说明理由.

28.在平面直角坐标系xOy中,已知动点P在正比例函数y=x的图象上,点P的横坐标为m(m>0)。以点P为圆心, 为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。
为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。
(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ。试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC-∠DBE的度数。
 为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。
为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ。试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC-∠DBE的度数。

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
