搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．
的绝对值为（ ）
的绝对值为（ ）| A．7 | B． | C． | D． |
2．随着交通网络的不断完善．旅游业持续升温，据统计，在今年“五一”期间，某风景区接待游客403000人，这个数据用科学记数法表示为（ ）
| A．403×103 | B．40.3×104 | C．4.03×105 | D．0.403×106 |
3．下列四个图形中，是三棱柱的平面展开图的是
A． | B． | C． | D． |
4．在下列实数中，无理数是( )
| A．0 | B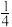． | C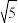． | D．6 |
5．已知⊙O1与⊙O2的半径分别为2cm和3cm，若O1O2=5cm．则⊙O1与⊙O2的位置关系是
| A．外离 | B．相交 | C．内切 | D．外切 |
6．下列运算正确的是
A． |
| B．x2•x3=x6 |
| C．（a+b）2=a2+b2 |
D． |
7．关于x的一元二次方程3x2﹣6x+m=0有两个不相等的实数根，则m的取值范围是
| A．m＜3 | B．m≤3 | C．m＞3 | D．m≥3 |
8．下列说法错误的是（ ）
| A．打开电视机，正在播放广告这一事件是随机事件 |
| B．要了解小赵一家三口的身体健康状况，适合采用抽样调查 |
| C．方差越大，数据的波动越大 |
| D．样本中个体的数目称为样本容量 |
9．甲、乙两个工程队共同承包某一城市美化工程，已知甲队单独完成这项工程需要30天，若由甲队先做10天，剩下的工程由甲、乙两队合作8天完成．问乙队单独完成这项工程需要多少天？若设乙队单独完成这项工程需要x天．则可列方程为
A． | B．10+8+x=30 | C． | D． |
10．等腰三角形的一个角是80°，则它的顶角的度数是（ ）
| A．80° | B．80°或20° | C．80°或50° | D．20° |
11．如图，图1、图2、图3分别表示甲、乙、丙三人由甲A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（ ）
| A．甲＜乙＜丙 | B．乙＜丙＜甲 | C．丙＜乙＜甲 | D．甲=乙=丙 |
12．定义：直线l1与l2相交于点O，对于平面内任意一点M，点M到直线l1、l2的距离分别为p、q，则称有序实数对（p，q）是点M的“距离坐标”，根据上述定义，“距离坐标”是（1，2）的点的个数是
| A．2 | B．3 | C．4 | D．5 |
13．比较大小：﹣1___ 2（填“＞”或“＜”）
14．当x=___ 时，分式
无意义．
无意义．15．请写出一个图形经过一、三象限的正比例函数的解析式___ ．
16．如图，DE是△ABC的中位线，则△ADE与△ABC的面积的比是___ ．
17．不等式组
的解集是 ．
的解集是 ．18．如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是___ ．
19．计算：
．
．20．如图，梯形ABCD中，AD∥BC，AB∥DE，∠DEC=∠C，求证：梯形ABCD是等腰梯形．
21．如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．
（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．
（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．
22．（1）我市开展了“寻找雷锋足迹”的活动，某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况，随机调查了七年级50名学生在一个月内做好事的次数，并将所得数据绘制成统计图，请根据图中提供的信息解答下列问题：
①所调查的七年级50名学生在这个月内做好事次数的平均数是 ，众数是 ，极差是 ：
②根据样本数据，估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数．
（2）甲口袋有2个相同的小球，它们分别写有数字1和2；乙口袋中装有3个相同的小球，它们分别写有数字3、4和5，从这两个口袋中各随机地取出1个小球．
①用“树状图法”或“列表法”表示所有可能出现的结果；
②取出的两个小球上所写数字之和是偶数的概率是多少？
①所调查的七年级50名学生在这个月内做好事次数的平均数是 ，众数是 ，极差是 ：
②根据样本数据，估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数．
（2）甲口袋有2个相同的小球，它们分别写有数字1和2；乙口袋中装有3个相同的小球，它们分别写有数字3、4和5，从这两个口袋中各随机地取出1个小球．
①用“树状图法”或“列表法”表示所有可能出现的结果；
②取出的两个小球上所写数字之和是偶数的概率是多少？
23．如图，一次函数y=ax+b的图象与反比例函数
的图象交于A（﹣2，m），B
（4，﹣2）两点，与x轴交于C点，过A作AD⊥x轴于D．
（1）求这两个函数的解析式：
（2）求△ADC的面积．
的图象交于A（﹣2，m），B（4，﹣2）两点，与x轴交于C点，过A作AD⊥x轴于D．
（1）求这两个函数的解析式：
（2）求△ADC的面积．
24．如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i=1：
，AB=10米，AE=15米．（i=1：是指坡面的铅直高度BH与水平宽度AH的比）
（1）求点B距水平面AE的高度BH；
（2）求广告牌CD的高度．
（测角器的高度忽略不计，结果精确到0.1米．参考数据：
1.414，
1.732）
，AB=10米，AE=15米．（i=1：是指坡面的铅直高度BH与水平宽度AH的比）（1）求点B距水平面AE的高度BH；
（2）求广告牌CD的高度．
（测角器的高度忽略不计，结果精确到0.1米．参考数据：
1.414，1.732）25．如图，在Rt△ABC中，∠A=90°，O是BC边上一点，以O为圆心的半圆与AB边相切于点D，与AC、BC边分别交于点E、F、G，连接OD，已知BD=2，AE=3，tan∠BOD=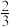
．
（1）求⊙O的半径OD；
（2）求证：AE是⊙O的切线；
（3）求图中两部分阴影面积的和．
．
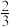（1）求⊙O的半径OD；
（2）求证：AE是⊙O的切线；
（3）求图中两部分阴影面积的和．
26．如图，在平面直角坐标系中，O为坐标原点，抛物线
与x轴相交于O、B，顶点为A，连接OA．
（1）求点A的坐标和∠AOB的度数；
（2）若将抛物线向右平移4个单位，再向下平移2个单位，得到抛物线m，其顶点为点C．连接OC和AC，把△AOC沿OA翻折得到四边形ACOC′．试判断其形状，并说明理由；
（3）在（2）的情况下，判断点C′是否在抛物线上，请说明理由；
（4）若点P为x轴上的一个动点，试探究在抛物线m上是否存在点Q，使以点O、P、C、Q为顶点的四边形是平行四边形，且OC为该四边形的一条边？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
与x轴相交于O、B，顶点为A，连接OA．
（1）求点A的坐标和∠AOB的度数；
（2）若将抛物线
向右平移4个单位，再向下平移2个单位，得到抛物线m，其顶点为点C．连接OC和AC，把△AOC沿OA翻折得到四边形ACOC′．试判断其形状，并说明理由；（3）在（2）的情况下，判断点C′是否在抛物线
上，请说明理由；（4）若点P为x轴上的一个动点，试探究在抛物线m上是否存在点Q，使以点O、P、C、Q为顶点的四边形是平行四边形，且OC为该四边形的一条边？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
