全一卷
1.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为_____ m


2.下列各数中,最小的实数是 …………………………………( )
A. | B.3 | C.0 | D. |
3.下列说法中,完全正确的是 ………………………………………………( )
| A.打开电视机,正在转播足球比赛 |
| B.抛掷一枚均匀的硬币,正面一定朝上 |
| C.三条任意长的线段都可以组成一个三角形 |
| D.从1,2,3,4,5这五个数字中任取一个数,取到奇数的可能性较大 |
4.图4中几何体的主视图为 …………………………………………( )

5.下列运算正确的是 ……………………………………………( )
A. | B. | C. | D. |
6.计算 的结果是 ……………………………( )
的结果是 ……………………………( )
 的结果是 ……………………………( )
的结果是 ……………………………( )| A.6 | B. | C.2 | D. |
7.在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕边AC所在直线旋转
一周得到圆锥,则该圆锥的侧面积是 ……………………………………( )
一周得到圆锥,则该圆锥的侧面积是 ……………………………………( )
A.25 | B.65 | C.90 | D.130 |
8.化简 的结果为 …………………………………( )
的结果为 …………………………………( )
 的结果为 …………………………………( )
的结果为 …………………………………( )A. | B. | C. | D.1 |
9.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用 ,
, 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法:

① ,②
,② ,③
,③ ,④
,④ .
.
其中说法正确的是 …………………………………………………………( )
 ,
, 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法:
①
 ,②
,② ,③
,③ ,④
,④ .
.其中说法正确的是 …………………………………………………………( )
| A.①② | B.①②③ | C.①②④ | D.①②③④ |
10.计算: .
.
 .
.11.如图,在□ABCD中,∠A=120°,则∠D= °.

12.要使分式 有意义,则
有意义,则 须满足的条件为 .
须满足的条件为 .
 有意义,则
有意义,则 须满足的条件为 .
须满足的条件为 .13.分解因式:
______ .

14.在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知袋中只有3个红球,且一次摸出一个球是红球的概率为 ,那么袋中的球共有 个.
,那么袋中的球共有 个.
 ,那么袋中的球共有 个.
,那么袋中的球共有 个.15.方程 的解为 .
的解为 .
 的解为 .
的解为 .16.现有甲、乙两支排球队,每支球队队员身高的平均数均为1.85米,方差分别为 ,
, ,则身高较整齐的球队是 队.
,则身高较整齐的球队是 队.
 ,
, ,则身高较整齐的球队是 队.
,则身高较整齐的球队是 队.17.写出一个既有轴对称性质又有中心对称性质的图形名称: .
18.如图,矩形ABCD中,AB=8cm,BC=4cm,E是DC的中点,BF= BC,则四边形DBFE的面积为
BC,则四边形DBFE的面积为  .
.
 BC,则四边形DBFE的面积为
BC,则四边形DBFE的面积为  .
.
19.如图,Rt△ABC在第一象限, ,AB=AC=2,点A在直线
,AB=AC=2,点A在直线 上,其中点A的横坐标为1,且AB∥
上,其中点A的横坐标为1,且AB∥ 轴,AC∥
轴,AC∥ 轴,若双曲线
轴,若双曲线
 与△
与△ 有交点,则k的取值范围是 .
有交点,则k的取值范围是 .
 ,AB=AC=2,点A在直线
,AB=AC=2,点A在直线 上,其中点A的横坐标为1,且AB∥
上,其中点A的横坐标为1,且AB∥ 轴,AC∥
轴,AC∥ 轴,若双曲线
轴,若双曲线
 与△
与△ 有交点,则k的取值范围是 .
有交点,则k的取值范围是 .
20.计算:

21.如图,点B和点C分别为∠MAN两边上的点,AB=AC.

(1)按下列语句画出图形:
① AD⊥BC,垂足为D;
② ∠BCN的平分线CE与AD的延长线交于点E
③ 连结BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形予以证明.

(1)按下列语句画出图形:
① AD⊥BC,垂足为D;
② ∠BCN的平分线CE与AD的延长线交于点E
③ 连结BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形予以证明.
22.如图,在平面直角坐标系中,梯形ABCD的顶点坐标分别为A ,B
,B ,
, ,D
,D ,将梯形ABCD绕点D逆时针旋转90°得到梯形
,将梯形ABCD绕点D逆时针旋转90°得到梯形 .
.

(1)在平面直角坐标系中画出梯形A1B1C1D,则
 的坐标为 ,
的坐标为 ,
 的坐标为 ,
的坐标为 ,
 的坐标为 ;
的坐标为 ;
(2)点C旋转到点 的路线长为 (结果保留
的路线长为 (结果保留 ).
).
 ,B
,B ,
, ,D
,D ,将梯形ABCD绕点D逆时针旋转90°得到梯形
,将梯形ABCD绕点D逆时针旋转90°得到梯形 .
.
(1)在平面直角坐标系中画出梯形A1B1C1D,则
 的坐标为 ,
的坐标为 , 的坐标为 ,
的坐标为 , 的坐标为 ;
的坐标为 ;(2)点C旋转到点
 的路线长为 (结果保留
的路线长为 (结果保留 ).
).23.计算-(-11)的结果是( ).
| A.11 | B.-11 | C. | D.- |
24.如图,立体图形的主视图是( )


A. | B. | C. | D. |
25.下列等式成立的是( ).
A. | B. | C. | D. |
26.三根木条的长度如图,能组成三角形的是( )

27.计算 结果是( ).
结果是( ).
 结果是( ).
结果是( ).| A.0 | B.1 | C.-1 | D.x |
28.
如图,小球从点A运动到点B,速度v(米/秒)和时间t(秒)的函数关系式是v=2t.

如果小球运动到点B时的速度为6米/秒,小球从点A到点B的时间是( ).
如图,小球从点A运动到点B,速度v(米/秒)和时间t(秒)的函数关系式是v=2t.

如果小球运动到点B时的速度为6米/秒,小球从点A到点B的时间是( ).
| A.1秒 | B.2秒 | C.3秒 | D.4秒 |
29.A、B、C、D四个班各选10名同学参加学校1 500米长跑比赛,各班选手平均用时及方差如下表:
各班选手用时波动性最小的是( ).
| 班 | A班 | B班 | C班 | D班 |
| 平均用时(分钟) | 5 | 5 | 5 | 5 |
| 方差 | 0.15 | 0.16 | 0.17 | 0.14 |
各班选手用时波动性最小的是( ).
| A.A班 | B.B班 | C.C班 | D.D班 |
30.甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.这些球除了颜色外没有其他区别.搅匀两箱中的球,从箱中分别任意摸出一个球.正确说法是( ).
| A.从甲箱摸到黑球的概率较大 |
| B.从乙箱摸到黑球的概率较大 |
| C.从甲、乙两箱摸到黑球的概率相等 |
| D.无法比较从甲、乙两箱摸到黑球的概率 |
31.如图,直线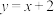 与双曲线
与双曲线 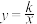 相交于点A,点A的纵坐标为3,k的值为( ).
相交于点A,点A的纵坐标为3,k的值为( ).

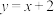 与双曲线
与双曲线 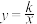 相交于点A,点A的纵坐标为3,k的值为( ).
相交于点A,点A的纵坐标为3,k的值为( ).
| A.1 | B.2 | C.3 | D.4 |
32.如图,直线 ,
, 与
与 和
和 分别相切于点
分别相切于点 和点
和点 .点
.点 和点
和点 分别是
分别是 和
和 上的动点,
上的动点, 沿
沿 和
和 平移.
平移. 的半径为
的半径为 ,
, .下列结论错误的是( ).
.下列结论错误的是( ).

 ,
, 与
与 和
和 分别相切于点
分别相切于点 和点
和点 .点
.点 和点
和点 分别是
分别是 和
和 上的动点,
上的动点, 沿
沿 和
和 平移.
平移. 的半径为
的半径为 ,
, .下列结论错误的是( ).
.下列结论错误的是( ).
A. | B.若 与 与 相切,则 相切,则 |
C.若 ,则 ,则 与 与 相切 相切 | D. 和 和 的距离为 的距离为 |
33.使 有意义的x取值范围是______.
有意义的x取值范围是______.
 有意义的x取值范围是______.
有意义的x取值范围是______.34.如图,□ABCD中,点A关于点O的对称点是点____.

35.在“抛掷正六面体”的试验中,如果正六面体的六个面分别标有数字“1”、“2”、“3”、“4”、“5”和“6”,如果试验的次数增多,出现数字“1”的频率的变化趋势是___________.
36.如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为_______.
37.计算:

38.如图,梯形ABCD中,AD∥BC,点M是BC的中点,且MA=MD.

求证:四边形ABCD是等腰梯形.

求证:四边形ABCD是等腰梯形.
39.电视台在南充城市某居民小区对电视节目的收视情况进行抽样调查,每人只能在被调查的五类电视节目中选择一类“最喜欢”的电视节目,将统计结果绘制了两幅不完整的统计图(图1,图2).请根据图中信息解答问题:

(1)这次抽样调查了多少人?
(2)在扇形统计图中,最喜欢娱乐节目对应的圆心角比最喜欢戏曲节目对应的圆心角大90°,调查中最喜欢娱乐节目比最喜欢戏曲节目的多多少人?
(3)估计南充城区有100万人中最喜欢体育节目的有多少人?

(1)这次抽样调查了多少人?
(2)在扇形统计图中,最喜欢娱乐节目对应的圆心角比最喜欢戏曲节目对应的圆心角大90°,调查中最喜欢娱乐节目比最喜欢戏曲节目的多多少人?
(3)估计南充城区有100万人中最喜欢体育节目的有多少人?
40.关于x的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围.
(2)请选择一个k的负整数值,并求出方程的根.
 有两个不相等的实数根.
有两个不相等的实数根.(1)求k的取值范围.
(2)请选择一个k的负整数值,并求出方程的根.
41.如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E

(1)求证:△ABD∽△CED
(2)若AB=6,AD=2CD,求BE的长.

(1)求证:△ABD∽△CED
(2)若AB=6,AD=2CD,求BE的长.
42.如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).

(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?

(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
43.如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE= BC.
BC.

(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
 BC.
BC.
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
44.
已知抛物线 上有不同的两点E
上有不同的两点E 和F
和F .
.

(1)求抛物线的解析式.
(2)如图,抛物线 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)当m,n为何值时,∠PMQ的边过点F.
已知抛物线
 上有不同的两点E
上有不同的两点E 和F
和F .
.
(1)求抛物线的解析式.
(2)如图,抛物线
 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.(3)当m,n为何值时,∠PMQ的边过点F.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
