搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．在实数0，－π，
，－4中，最小的数是（ ）
，－4中，最小的数是（ ）| A．0 | B．－π | C． | D．－4 |
2．2011年3月11日，日本发生了里氏9.0级大地震，导致当天地球自转时间减少了0.0000016秒，将0.0000016用科学记数法表示为（）
A． | B． | C． |
3．下列运算正确的是（ ）
| A．x3+x2=2x6 | B．3x3÷x=2x2 | C．x4•x2=x8 | D．（x3）2=x6 |
4．四张完全相同的卡片上分别画有平行四边形、菱形、等腰梯形、圆，现从中任意抽取一张，卡片上所画的图形恰好是中心对称图形的概率为（）
A． | B．1 | C． | D． |
5．下图是一个由多个相同小正方体堆积而成的几何体的俯视图，图中所示数字为该位置小正方体的个数，则这个几何体的左视图是（ ）
A． | B． | C． | D． |
6．如图，已知OA=OB=OC且∠ACB=30º，则∠AOB的大小是( )
| A．40º | B．50º | C．60º | D．70º |
7．把抛物线
的图像向右平移3个单位，再向上平移2个单位，所得到的图象的解析式为
，则b的值为【 】
的图像向右平移3个单位，再向上平移2个单位，所得到的图象的解析式为
，则b的值为【 】| A．2 | B．4 | C．6 | D．8 |
8．直线
与反比例函数
的图象（x<0）交于点A，与x轴相交于点B，过点B作x轴垂线交双曲线于点C，若AB=AC，则k的值为【 】
与反比例函数
的图象（x<0）交于点A，与x轴相交于点B，过点B作x轴垂线交双曲线于点C，若AB=AC，则k的值为【 】
| A．－2 | B．－4 | C．－6 | D．－8 |
9．如图，四边形OABC为菱形，点A、B在以O为圆心的弧上，若OA=2，∠1=∠2，则扇形ODE的面积为【 】
A.
B.
C.
D.
A.
B.
C.
D.
10．在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1,………按这样的规律进行下去，第2012个正方形的面积为【 】
A． | B． | C． | D． |
11．分解因式：2a3﹣8a=________ ．
12．设x1、x2是一元二次方程x2＋5x－3=0的两个实根，且
，则a=_______
，则a=13．如图，
ABCD 中，AE⊥BC于E，AF⊥CD于F，若AE=4，AF=6，sin∠BAE=
，则CF=_______ .
ABCD 中，AE⊥BC于E，AF⊥CD于F，若AE=4，AF=6，sin∠BAE=
，则CF=
14．若关于x的不等式组
的解集为x<2，则a的取值范围是_______ .
的解集为x<2，则a的取值范围是15．在锐角三角形
中 ，
，
，
平分
，M、N分别是、
上的动点，则
的最小值是_______ ．
中 ，，，平分，M、N分别是、上的动点，则的最小值是16．.某私营服装厂根据2011年市场分析，决定2012年调整服装制作方案，准备每周（按120工时计算）制作西服、休闲服、衬衣共360件，且衬衣至少60件。已知每件服装的收入和所需工时如下表：
设每周制作西服x件，休闲服y件，衬衣z件。
（1）请你分别从件数和工时数两个方面用含有x,y 的代数式表示衬衣的件数z,
（2）求y与x之间的函数关系式。
（3）问每周制作西服、休闲服、衬衣各多少件时，才能使总收入最高？最高总收入是多少？
| 服装名称 | 西服 | 休闲服 | 衬衣 |
| 工时/件 |  | |  |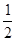
| 收入（百元）/件 | 3 | 2 | 1 |
（1）请你分别从件数和工时数两个方面用含有x,y 的代数式表示衬衣的件数z,
（2）求y与x之间的函数关系式。
（3）问每周制作西服、休闲服、衬衣各多少件时，才能使总收入最高？最高总收入是多少？
17．已知：如图一，抛物线y=ax2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y=x-2经过A、C两点，且AB=2．
（1）求抛物线的解析式；
（2）若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s=
，当t为何值时，s有最小值，并求出最小值．
（3）在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．
（1）求抛物线的解析式；
（2）若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移，且分别交y轴、线段BC于点E，D，同时动点P从点B出发，沿BO方向以每秒2个单位速度运动，（如图2）；当点P运动到原点O时，直线DE与点P都停止运动，连DP，若点P运动时间为t秒；设s=
，当t为何值时，s有最小值，并求出最小值．（3）在（2）的条件下，是否存在t的值，使以P、B、D为顶点的三角形与△ABC相似；若存在，求t的值；若不存在，请说明理由．
