全一卷
1.点M(1,2)关于x轴对称的点的坐标为 ( )。
| A.(—1,2) | B.(-1,-2) | C.(1,-2) | D.(2,-1) |
2.等腰三角形的底角与顶角的度数之比为2∶1,则顶角为( ).
| A.72° | B.36° | C.36°或72° | D.18° |
3.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )


| A.40° | B.60° | C.45° | D.50° |
4.在实数5、 、
、 、
、 中,无理数是( ).
中,无理数是( ).
 、
、 、
、 中,无理数是( ).
中,无理数是( ).| A.5 | B. | C. | D. |
5.已知 ,则代数式
,则代数式 的值为
的值为_________ .
 ,则代数式
,则代数式 的值为
的值为6.(本题满分12分)如图,过A(8,0)、B(0, )两点的直线与直线
)两点的直线与直线 交于点C.平行于
交于点C.平行于 轴的直线
轴的直线 从原点O出发,以每秒1个单位长度的速度沿
从原点O出发,以每秒1个单位长度的速度沿 轴向右平移,到C点时停止;
轴向右平移,到C点时停止; 分别交线段BC、OC于点D、E,以DE为边向左侧作等边△
分别交线段BC、OC于点D、E,以DE为边向左侧作等边△ DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线
DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线 的运动时间为t(
的运动时间为t( 秒).
秒).
(1)直接写出C点坐标和t的取值范围;
(2)求S与t的函数关系式;
(3)设直线 与
与 轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
 )两点的直线与直线
)两点的直线与直线 交于点C.平行于
交于点C.平行于 轴的直线
轴的直线 从原点O出发,以每秒1个单位长度的速度沿
从原点O出发,以每秒1个单位长度的速度沿 轴向右平移,到C点时停止;
轴向右平移,到C点时停止; 分别交线段BC、OC于点D、E,以DE为边向左侧作等边△
分别交线段BC、OC于点D、E,以DE为边向左侧作等边△ DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线
DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线 的运动时间为t(
的运动时间为t( 秒).
秒).(1)直接写出C点坐标和t的取值范围;
(2)求S与t的函数关系式;
(3)设直线
 与
与 轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
7.多项式 为____ 次_____ 项式.最高次项系数是__________.
为____ 次_____ 项式.最高次项系数是__________.
 为____ 次_____ 项式.最高次项系数是__________.
为____ 次_____ 项式.最高次项系数是__________.8.有10张形状、大小都一样的卡片,分别写有1至10十个数,将它们背面朝上洗匀后,任意抽一张,抽得偶数的成功率为_____________.
9.计算: .
.
 .
.10.正多边形的每个内角等于 ,则这个正多边形的边数为______________条.
,则这个正多边形的边数为______________条.
 ,则这个正多边形的边数为______________条.
,则这个正多边形的边数为______________条.11.下列说法正确的是( )
| A.正数和负数互为相反数 | B. 的相反数是正数 的相反数是正数 |
| C.任何有理数的绝对值都大于它本身 | D.任何一个有理数都有相反数 |
12.下列各式中运算正确的是()
A. | B. |
C. | D. |
13.整式 去括号应为( )
去括号应为( )
 去括号应为( )
去括号应为( )A. | B. | C. | D. |
14.你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸再捏合,再拉伸,……反复几次,就把这根很粗的面条拉成了许多细的面条,如下面的草图所示

这种捏合到第7次后可拉出细面条( )

这种捏合到第7次后可拉出细面条( )
| A.14根 | B.49根 | C.64根 | D.128根 |
15.一元二次方程 的解是 ( ).
的解是 ( ).
 的解是 ( ).
的解是 ( ).A. , , | B. , , |
C. , , | D. , , |
16.(本题满分8分) 求证:矩形的对角线相等.
17.(本题满分6分)
先化简,再求值: ,其中
,其中
先化简,再求值:
 ,其中
,其中
18.化简 的结果是 ( )
的结果是 ( )
 的结果是 ( )
的结果是 ( )A. | B. | C. | D. |
19.
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
20.若式子 在实数范围内有意义,则x的取值范围是()
在实数范围内有意义,则x的取值范围是()
 在实数范围内有意义,则x的取值范围是()
在实数范围内有意义,则x的取值范围是()| A.x>5 | B.x≥5 | C.x≠5 | D.x≥0 |
21.等腰三角形的一个内角为50°,则另外两个角的度数分别为( )
| A.65°,65° | B.50°,80° | C.65°,65°或50°,80° | D. 50°,50° |
22.如图,已知∠1=∠2,请你添加一个条件:______ _____,使△ABD≌△ACD。

23.如下图,半径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O′,点O′的坐标是 



24.某数值转换器的程序如图所示,当输入的x为16时,输出的y是




25..(9分) 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
(1) 先出发,先出发 分钟。
先到达终点,先到 分钟。
(2) 在什么时间段内,两人均行驶在途中(不包括起点和终点),在这一时间段内,请你根据下列情形填空:
当 时,甲在乙的前面时;
当 时,甲与乙相遇时;
当 时,甲在乙后面.
(3) 分别求出甲、乙两人的行驶速度;
(1) 先出发,先出发 分钟。
先到达终点,先到 分钟。
(2) 在什么时间段内,两人均行驶在途中(不包括起点和终点),在这一时间段内,请你根据下列情形填空:
当 时,甲在乙的前面时;
当 时,甲与乙相遇时;
当 时,甲在乙后面.
(3) 分别求出甲、乙两人的行驶速度;
26.(8分)国际比赛的足球场地是在100米到110米之间,宽是在64米到75米之间,现有一个长方形的足球场,其长是宽的1.5倍,面积是7560平方米,那么这个足球场能用作国际比赛吗?(参考数据: )
)

 )
)
27.(本题满分6分)计算: 4cos30°+
4cos30°+
 4cos30°+
4cos30°+
28.正五边形的内角和等于______度.
29.情系玉树大爱无疆,截至5月21日12时,青海玉树共接收国内外地震救灾捐赠款物551300万元,将551300万元用科学记数法表示为__________万元.
30.如果1≤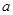 ≤
≤ ,则
,则 的值是 ( )
的值是 ( )
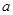 ≤
≤ ,则
,则 的值是 ( )
的值是 ( )A. | B. | C. | D.1 |
31.下列运算正确的是( ).
A.  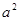 = = | B. | C. | D. |
32.(本题满分10分)
(1)(本小题满分4分) —
— +
+

(2)(本小题满分6分)已知:y=y1+y2,y1与x2成正比例,y2与x成反比例,且
x=1时,y=3;x=-1时,y=1. 求x=- 时,y的值.
时,y的值.
(1)(本小题满分4分)
 —
— +
+

(2)(本小题满分6分)已知:y=y1+y2,y1与x2成正比例,y2与x成反比例,且
x=1时,y=3;x=-1时,y=1. 求x=-
 时,y的值.
时,y的值.33. 的倒数是( )
的倒数是( )
 的倒数是( )
的倒数是( )A. | B. | C. | D. |
34. 的绝对值是( ).
的绝对值是( ).
 的绝对值是( ).
的绝对值是( ).A. | B.2 | C. | D. |
35.如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( ).


| A.1:2 | B.1:4 |
| C.2:1 | D.4:1 |
36.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( ).


| A.∠1 | B.∠2 |
| C.∠4 | D.∠5 |
37.如图所示几何体的左视图是().
A. | B. | C. | D. |
38.下列说法正确的是( ).
| A.买一张福利彩票一定中奖,是必然事件. |
| B.买一张福利彩票一定中奖,是不可能事件. |
C.抛掷一个正方体骰子,点数为奇数的概率是 . . |
| D.一组数据:1,7,3,5,3的众数是3. |
39.如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________ .


40.(本题满分8分)如图是某地6月1日至6月7日每天最高、最低气温的折线统计图.
请你根据折线统计图,回答下列问题:
(1)在这7天中,日温差最大的一天是6月_____日;
 (2)这7天的日最高气温的平均数是______℃;
(2)这7天的日最高气温的平均数是______℃;
(3)这7天日最高气温的方差是 _______ .
请你根据折线统计图,回答下列问题:
(1)在这7天中,日温差最大的一天是6月_____日;
 (2)这7天的日最高气温的平均数是______℃;
(2)这7天的日最高气温的平均数是______℃;(3)这7天日最高气温的方差是 _______ .

41.如图,已知正方形ABCD的边长为4 ,E是BC边上的一个动点,AE⊥EF, EF交DC于F, 设BE= ,FC=
,FC= ,则当点E从点B运动到点C时,
,则当点E从点B运动到点C时, 关于
关于 的函数图象是( )
的函数图象是( )

 ,FC=
,FC= ,则当点E从点B运动到点C时,
,则当点E从点B运动到点C时, 关于
关于 的函数图象是( )
的函数图象是( )
A. | B. | C. | D. |
42.将抛物线 绕它的顶点旋转180°,所得抛物线的解析式是( ).
绕它的顶点旋转180°,所得抛物线的解析式是( ).
 绕它的顶点旋转180°,所得抛物线的解析式是( ).
绕它的顶点旋转180°,所得抛物线的解析式是( ).A. | B. |
C. | D. |
43.函数 的自变量
的自变量 的取值范围是 .
的取值范围是 .
 的自变量
的自变量 的取值范围是 .
的取值范围是 .44.(本题满分8分)
某蔬菜公司收购到某种蔬菜104吨,准备加工后上市销售. 该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?
某蔬菜公司收购到某种蔬菜104吨,准备加工后上市销售. 该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?
45.若反比例函数 的图象经过点(-3,2),则
的图象经过点(-3,2),则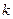 的值为( ).
的值为( ).
 的图象经过点(-3,2),则
的图象经过点(-3,2),则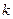 的值为( ).
的值为( ).| A.-6 | B.6 | C.-5 | D.5 |
46.因式分解: =" " .
=" " .
 =" " .
=" " .47.如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.

(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.

48.一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是 ( ).


A. | B. |
C. | D. |
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
