全一卷
1.下列实数中的无理数是( )
| A.0.7 | B. | C.π | D.-8 |
2.如图是3个相同的小正方体组合而成的几何体,它的俯视图是( )


A. | B. | C. | D. |
3.如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )


| A.同位角 | B.内错角 |
| C.同旁内角 | D.对顶角 |
4.下列算式中,结果等于 的是( )
的是( )
 的是( )
的是( )A. | B. | C. | D. |
5.不等式组 的解集是()
的解集是()
 的解集是()
的解集是()| A.x>-1 | B.x>3 | C.-1<x<3 | D.x<3 |
6.下列说法中,正确的是( )
| A.不可能事件发生的概率为0 |
B.随机事件发生的概率为 |
| C.概率很小的事件不可能发生 |
| D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 |
7.A,B是数轴上两点,线段AB上的点表示的数中,有互为相反数的是( )
A. | B. |
C. | D. |
8.平面直角坐标系中,已知□ABCD的三个顶点坐标分别是A(m,n),B ( 2,-l ),C(-m,-n),则点D的坐标是( )
| A.(-2 ,l ) | B.(-2,-l ) | C.(-1,-2 ) D .(-1,2 ) |
9.如图,以原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )

 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
| A.(sinα,sinα) | B.(cosα,cosα) | C.(cosα,sinα) | D.(sinα,cosα) |
10.下表是某校合唱团成员的年龄分布

对于不同的x,下列关于年龄的统计量不会发生改变的是()

对于不同的x,下列关于年龄的统计量不会发生改变的是()
| A.平均数,中位数 | B.众数,中位数 |
| C.平均数,方差 | D.中位数,方差 |
11.已知点A(﹣1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可以是( )
A. | B. | C. | D. |
12.下列选项中,能使关于x的一元二次方程ax2﹣4x+c=0一定有实数根的是( )
| A.a>0 | B.a=0 | C.c>0 | D.c=0 |
13.分解因式:a2-4=________ .
14.若二次根式 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 .
 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 .15.已知四个点的坐标分别是(-1,1),(2,2),( ,
, ),(-5,-
),(-5,- ),从中随机选一个点,在反比例函数y=
),从中随机选一个点,在反比例函数y= 图象上的概率是 .
图象上的概率是 .
 ,
, ),(-5,-
),(-5,- ),从中随机选一个点,在反比例函数y=
),从中随机选一个点,在反比例函数y= 图象上的概率是 .
图象上的概率是 .16.如图所示的两段弧中,位于上方的弧半径为 ,下方的弧半径为
,下方的弧半径为 ,则
,则
 .(填“>“,”“=”“<”)
.(填“>“,”“=”“<”)
 ,下方的弧半径为
,下方的弧半径为 ,则
,则
 .(填“>“,”“=”“<”)
.(填“>“,”“=”“<”)
17.若x+y=10,xy=1 ,则 =
=_________ .
 =
=18.如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是_____ .


19.计算: .
.
 .
.20.化简: .
.
 .
.21.一个平分角的仪器如图所示,其中AB=AD,BC=DC,求证:∠BAC=∠DAC .


22.某班去看演出,甲种票每张24元,乙种票每张18元.如果35名学生购票恰好用去750元,甲、乙两种票各买了多少张?
23.福州市2011~2015年常住人口数统计如图所示.

根据图中提供的信息,回答下列问题:
(1)福州市常住人口数,2015年比2014年增加了 万人;
(2)与上一年相比,福州市常住人口数增加最多的年份是 年;
(3)预测2016年福州市常住人口数大约为多少万人?请用所学的统计知识说明理由.

根据图中提供的信息,回答下列问题:
(1)福州市常住人口数,2015年比2014年增加了 万人;
(2)与上一年相比,福州市常住人口数增加最多的年份是 年;
(3)预测2016年福州市常住人口数大约为多少万人?请用所学的统计知识说明理由.
24.如图,正方形ABCD内接于⊙O,M为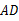 中点,连接BM,CM.
中点,连接BM,CM.
(1)求证:BM=CM;
(2)当⊙O的半径为2时,求 的长.
的长.
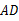 中点,连接BM,CM.
中点,连接BM,CM.(1)求证:BM=CM;
(2)当⊙O的半径为2时,求
 的长.
的长.
25.如图,在△ABC中,AB=AC=1,BC= ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC•CD的大小关系;
(2)求∠ABD的度数.

 ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.(1)通过计算,判断AD2与AC•CD的大小关系;
(2)求∠ABD的度数.

26.如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.

(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.

(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
27.已知,抛物线 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线
 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;(3)当点A在抛物线
 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
