全一卷
1.下列关于x的方程中,一定是一元二次方程的为( )
| A.x2-2=(x+3)2 | B.x2 1=0 1=0 | C.x2+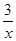 −5=0 −5=0 | D.ax2+bx+c=0 |
2.如果2是一元二次方程x2=x+c的一个根,那么c的值为( )
| A.2 | B.-2 | C.4 | D.-4 |
3.下列一元二次方程没有实数根的是( )
| A.x2+x+2=0 | B.x2+2x+1=0 | C.x2﹣1=0 | D.x2﹣2x﹣1=0 |
4.在平面直角坐标系中,若⊙O的半径是5,圆心O的坐标是(0,0),点P的坐标是(4,3),则点P与⊙O的位置关系是( )
| A.点P在⊙O内 | B.点P在⊙O上 | C.点P在⊙O外 | D.无法确定 |
5.若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为 ( )
| A.120° | B.180° | C.240° | D.300° |
6.如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
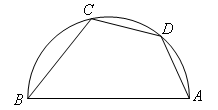

| A.55° | B.60° | C.65° | D.70° |
7.如图,以AB为直径的半圆绕A点,逆时针旋转60o,点B旋转到点B’的位置,已知AB=6,则图中阴影部分的面积为( )
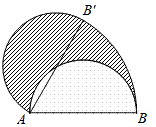

A.6 | B.5 | C.4 | D.3 |
8.把方程3x(x﹣1)=(x+2)(x﹣2)+9化成ax2+bx+c=0的形式为_____ .
9.若关于x的一元二次方程(m﹣1)x2+5x+m2﹣3m+2=0的常数项为0,则m的值等于_____ .
10.已知方程(2a-1)x2-8x+6=0没有实数根,则a的最小整数值是_______________.
11.若矩形的长是6cm,宽是3cm,一个正方形的面积等于该矩形的面积,则正方形的边长是_____________.
12.圆心O到直线l的距离为d,⊙O的半径为r,当d、r是方程x2-4x+m=0的根,且直线与⊙O相切时,m的值为__________________ .
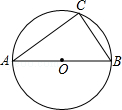
13.如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是__ .

14.如图,在正六边形ABCDEF中,连接AD,AE,则∠DAE=__________________度.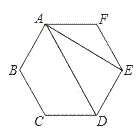

15.如图,AD为⊙O的直径,∠ABC=75°,且AC=BC,则∠BED=____________度.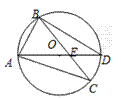

16.如图,如果从半径为9的圆形纸片剪去 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为_________________.
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为_________________.
 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为_________________.
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为_________________.
17.如图,平面直角坐标系中,O为坐标原点,以O为圆心作⊙O,点A、C分别是⊙O 与x轴负半轴、y轴正半轴的交点,点B、D在⊙O上,那么∠ADC的度数是__________________ .


18.解下列方程
(1)x2-3x+1=0(用公式法)
(2)x2+2x-3=0(用配方法)
(3)x(x+1)=2(x+1)
(4)
(1)x2-3x+1=0(用公式法)
(2)x2+2x-3=0(用配方法)
(3)x(x+1)=2(x+1)
(4)

19.已知关于x的一元二次方程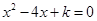 有两个实数根.
有两个实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程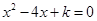 与
与 有一个相同的根,求常数m的值.
有一个相同的根,求常数m的值.
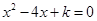 有两个实数根.
有两个实数根.(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程
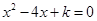 与
与 有一个相同的根,求常数m的值.
有一个相同的根,求常数m的值.20.如图,已知四边形ABCD内接于⊙O,E是AD延长线上一点,且AC=BC,求证:DC平分∠BDE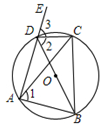

21.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.如图,将△ABC放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,作出△ABC的最小覆盖圆,并求出这个圆的半径.(保留作图痕迹)

22.果农李明种植的草莓计划以每千克15元的单价对外批发销售,由于部分果农盲目扩大种植,造成该草莓滞销.李明为了加快销售,减少损失,对价格经过两次下调后,以每千克9.6元的单价对外批发销售.
(1)求李明平均每次下调的百分率;
(2)小刘准备到李明处购买3吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金400元.
试问小刘选择哪种方案更优惠,请说明理由.
(1)求李明平均每次下调的百分率;
(2)小刘准备到李明处购买3吨该草莓,因数量多,李明决定再给予两种优惠方案以供其选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金400元.
试问小刘选择哪种方案更优惠,请说明理由.
23.已知一个包装盒的表面展开图如图.
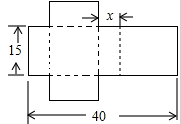
(1)若此包装盒的容积为1125cm3,请列出关于x的方程,并求出x的值;
(2)是否存在这样的x的值,使得次包装盒的容积为1800cm3?若存在,请求出相应的x的值;若不存在,请说明理由.
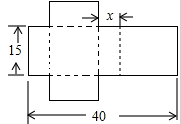
(1)若此包装盒的容积为1125cm3,请列出关于x的方程,并求出x的值;
(2)是否存在这样的x的值,使得次包装盒的容积为1800cm3?若存在,请求出相应的x的值;若不存在,请说明理由.
24.已知⊙O的半径为5,D是半圆弧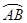 上一动点(不与A,B重合),以AD,AB为邻边作
上一动点(不与A,B重合),以AD,AB为邻边作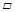 ABC
ABC
(1)如图1,当CD与⊙O相切时,求∠A的度数;
(2)如图2,当AD=6时,边CD与⊙O交于另一点E,求CE的长;
(3)若直线CD交⊙O于另一点E,当DE=6时,求AD的长.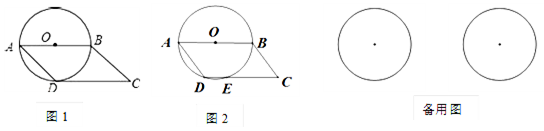
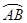 上一动点(不与A,B重合),以AD,AB为邻边作
上一动点(不与A,B重合),以AD,AB为邻边作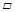 ABC
ABC| A. |

(2)如图2,当AD=6时,边CD与⊙O交于另一点E,求CE的长;
(3)若直线CD交⊙O于另一点E,当DE=6时,求AD的长.

25.如图, 为⊙
为⊙ 的直径,
的直径, ,且
,且 ,则
,则
______ .

 为⊙
为⊙ 的直径,
的直径, ,且
,且 ,则
,则

26.下列一元二次方程没有实数根的是( )
A. | B. | C. | D. |
27.如图,从半径为9cm的圆形纸片上剪去 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为____ cm.

 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
