全一卷
1.3的相反数是()
| A.-3 | B. | C. | D.3 |
2.如图,由四个正方体组成的几何体的左视图是( )


A. | B. | C. | D. |
3.用科学计数法表示136 000,其结果是()
A. | B. | C. | D. |
4.化简 的结果是()
的结果是()
 的结果是()
的结果是()A. | B. | C. | D. |
5.下列关于图形对称性的命题,正确的是( )
| A.圆既是轴对称性图形,又是中心对称图形 |
| B.正三角形既是轴对称图形,又是中心对称图形 |
| C.线段是轴对称图形,但不是中心对称图形 |
| D.菱形是中心对称图形,但不是轴对称图形 |
6.不等式组: 的解集是()
的解集是()
 的解集是()
的解集是()A. | B. | C. | D. |
7.某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )


| A.10,15 | B.13,15 | C.13,20 | D.15,15 |
8.如图,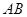 是
是 的直径,
的直径, 是
是 上位于
上位于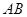 异侧的两点.下列四个角中,一定与
异侧的两点.下列四个角中,一定与 互余的角是()
互余的角是()

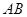 是
是 的直径,
的直径, 是
是 上位于
上位于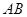 异侧的两点.下列四个角中,一定与
异侧的两点.下列四个角中,一定与 互余的角是()
互余的角是()
A. | B. | C. | D. |
9.若直线 经过点
经过点 和
和 ,且
,且 ,则
,则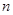 的值可以是()
的值可以是()
 经过点
经过点 和
和 ,且
,且 ,则
,则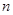 的值可以是()
的值可以是()| A.3 | B.4 | C.5 | D.6 |
10.如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )


| A.1区 | B.2区 | C.3区 | D.4区 |
11.计算
_________ .

12.如图,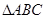 中,
中, 分别是
分别是 的中点,连线
的中点,连线 ,若
,若 ,则线段
,则线段 的长等于 .
的长等于 .
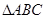 中,
中, 分别是
分别是 的中点,连线
的中点,连线 ,若
,若 ,则线段
,则线段 的长等于 .
的长等于 .
13.一个箱子装有除颜色外都相同的2个白球,2个黄球,1个红球.现添加同种型号的1个球,使得从中随机抽取1个球,这三种颜色的球被抽到的概率都是 ,那么添加的球是
,那么添加的球是_________ .
 ,那么添加的球是
,那么添加的球是14.已知 是数轴上的三个点,且C在B的右侧.点
是数轴上的三个点,且C在B的右侧.点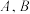 表示的数分别是1,3,如图所示.若
表示的数分别是1,3,如图所示.若 ,则点C表示的数是
,则点C表示的数是_________ .

 是数轴上的三个点,且C在B的右侧.点
是数轴上的三个点,且C在B的右侧.点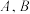 表示的数分别是1,3,如图所示.若
表示的数分别是1,3,如图所示.若 ,则点C表示的数是
,则点C表示的数是
15.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于 ______ 度.


16.已知矩形ABCD的四个顶点均在反比例函数 的图象上,且点A的横坐标是2,则矩形ABCD的面积为
的图象上,且点A的横坐标是2,则矩形ABCD的面积为_________ .
 的图象上,且点A的横坐标是2,则矩形ABCD的面积为
的图象上,且点A的横坐标是2,则矩形ABCD的面积为17.先化简,再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.18.如图,点 在一条直线上,
在一条直线上, .求证:
.求证: .
.
 在一条直线上,
在一条直线上, .求证:
.求证: .
.
19.如图,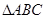 中,
中, ,垂足为
,垂足为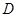 .求作
.求作 的平分线,分别交
的平分线,分别交 于
于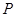 ,
,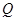 两点;并证明
两点;并证明 .(要求:尺规作图,保留作图痕迹,不写作法)
.(要求:尺规作图,保留作图痕迹,不写作法)
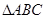 中,
中, ,垂足为
,垂足为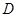 .求作
.求作 的平分线,分别交
的平分线,分别交 于
于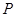 ,
,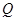 两点;并证明
两点;并证明 .(要求:尺规作图,保留作图痕迹,不写作法)
.(要求:尺规作图,保留作图痕迹,不写作法)
20.我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”其大意是:“有若干只鸡和兔关在同一笼子里,它们一共有35个头,94条腿.问笼中的鸡和兔各有多少只?”试用列方程(组)解应用题的方法求出问题的解.
21.如图,四边形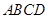 内接于
内接于 ,
,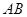 是
是 的直径,点
的直径,点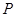 在
在 的延长线上,
的延长线上, .
.

(Ⅰ)若 ,求弧
,求弧 的长;
的长;
(Ⅱ)若弧 弧
弧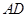 ,
, ,求证:
,求证: 是
是 的切线.
的切线.
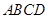 内接于
内接于 ,
,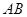 是
是 的直径,点
的直径,点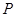 在
在 的延长线上,
的延长线上, .
.
(Ⅰ)若
 ,求弧
,求弧 的长;
的长;(Ⅱ)若弧
 弧
弧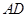 ,
, ,求证:
,求证: 是
是 的切线.
的切线.22.小明在某次作业中得到如下结果:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
据此,小明猜想:对于任意锐角 ,均有
,均有 .
.
(Ⅰ)当 时,验证
时,验证 是否成立;
是否成立;
(Ⅱ)小明的猜想是否成立?若成立,若成立,请给予证明;若不成立,请举出一个反例.
 ,
, ,
, ,
, ,
, .
.据此,小明猜想:对于任意锐角
 ,均有
,均有 .
.(Ⅰ)当
 时,验证
时,验证 是否成立;
是否成立;(Ⅱ)小明的猜想是否成立?若成立,若成立,请给予证明;若不成立,请举出一个反例.
23.自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
(Ⅰ)写出 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
| 使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
| 累计车费 | 0 | 0.5 | 0.9 | 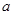 | 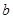 | 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
| 使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出
 的值;
的值;(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
24.如图,矩形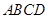 中,
中, ,
, 分别是线段AC、BC上的点,且四边形
分别是线段AC、BC上的点,且四边形 为矩形.
为矩形.

(Ⅰ)若 是等腰三角形时,求
是等腰三角形时,求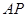 的长;
的长;
(Ⅱ)若 ,求
,求 的长.
的长.
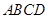 中,
中, ,
, 分别是线段AC、BC上的点,且四边形
分别是线段AC、BC上的点,且四边形 为矩形.
为矩形.
(Ⅰ)若
 是等腰三角形时,求
是等腰三角形时,求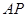 的长;
的长;(Ⅱ)若
 ,求
,求 的长.
的长.25.已知直线 与抛物线
与抛物线 有一个公共点
有一个公共点 ,且
,且 .
.
(Ⅰ)求抛物线顶点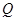 的坐标(用含
的坐标(用含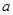 的代数式表示);
的代数式表示);
(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为 .
.
(ⅰ)若 ,求线段
,求线段 长度的取值范围;
长度的取值范围;
(ⅱ)求 面积的最小值.
面积的最小值.
 与抛物线
与抛物线 有一个公共点
有一个公共点 ,且
,且 .
.(Ⅰ)求抛物线顶点
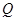 的坐标(用含
的坐标(用含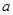 的代数式表示);
的代数式表示);(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为
 .
.(ⅰ)若
 ,求线段
,求线段 长度的取值范围;
长度的取值范围;(ⅱ)求
 面积的最小值.
面积的最小值. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
