搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．﹣3的绝对值是（ ）
| A．﹣3 | B．3 | C．- | D． |
2．已知一个几何体的三种视图如图所示，则该几何体是（）
| A．三棱柱 | B．三棱锥 | C．圆锥 | D．圆柱 |
3．如图，点M在线段AB上，则下列条件不能确定M是AB中点的是（ ）
A．BM= AB | B．AM+BM=AB | C．AM=BM | D．AB=2AM |
4．在△ABC中，AB=5，AC=8，则BC长不可能是（）
| A．4 | B．8 | C．10 | D．13 |
5．下列计算正确的是（ ）
| A．﹣5+2=﹣7 | B．6÷（﹣2）=﹣3 | C．（﹣1）2017=1 | D．﹣20=1 |
6．如图所示的分式化简，对于所列的每一步运算，依据错误的是（）
| A．①：同分母分式的加减法法则 | B．②：合并同类项法则 |
| C．③：提公因式法 | D．④：等式的基本性质 |
7．某创意工作室6位员工的月工资如图所示，因业务需要，现决定招聘一名新员工，若新员工的工资为4500元，则下列关于现在7位员工工资的平均数和方差的说法正确的是（）
| A．平均数不变，方差变大 | B．平均数不变，方差变小 |
| C．平均数不变，方差不变 | D．平均数变小，方差不变 |
8．如图，直线l是一次函数y=kx+b的图象，若点A（3，m）在直线l上，则m的值是（ ）
| A．﹣5 | B． | C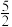． | D．7 |
9．函数y=x3﹣3x的图象如图所示，则以下关于该函数图象及其性质的描述正确的是（ ）
| A．函数最大值为2 | B．函数图象最低点为（1，﹣2） |
| C．函数图象关于原点对称 | D．函数图象关于y轴对称 |
10．如图，在
中，
，点D，E分别在边
和
上，若
，则下列结论错误的是 ( )
中，，点D，E分别在边和上，若，则下列结论错误的是 ( ) A． | B． | C． | D． |
11．2016年9月26日，我国自主设计建造的世界最大球面射电望远镜落成启用．该望远 镜理论上能接收到13 700 000 000光年以外的电磁信号．数据13 700 000 000光年用科学记数法表示为 光年．
12．一元二次方程x（x+3）=0的根是 ．
13．若矩形的面积为a2+ab，长为a+b，则宽为 _____ ．
14．甲、乙两位同学参加物理实验考试，若每人只能从A、B、C、D四个实验中随机抽取一个，则甲、乙两位同学抽到同一实验的概率为．
15．将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合，当α最小时，点A运动的路径长为．
16．如图，在平面直角坐标系中，菱形OABC的边OA在x轴上，AC与OB交于点D （8，4），反比例函数y=
的图象经过点
的图象经过点A．若将菱形OABC向左平移n个单位，使点C落在该反比例函数图象上，则n的值为 |
17．化简并求值：x（x﹣2）+（x+1）2，其中x=﹣2．
18．已知：不等式
≤2+x
（1）解该不等式，并把它的解集表示在数轴上；
（2）若实数a满足a＞2，说明a是否是该不等式的解．
≤2+x（1）解该不等式，并把它的解集表示在数轴上；
（2）若实数a满足a＞2，说明a是否是该不等式的解．
19．如图，E，F为平行四边形ABCD的对角线BD上的两点，AE⊥BD于点E，CF⊥BD于点F．
求证：AE=CF．
求证：AE=CF．
20．小明作业本中有一页被墨水污染了，已知他所列的方程组是正确的．写出题中被墨水污染的条件，并求解这道应用题．
21．某初中学校组织200位同学参加义务植树活动，每人植树的棵数在5至10之间．甲、乙两位同学分别调查了30位同学的植树情况，并将收集的数据进行了整理，绘制成统计表分别为表1和表2：
表1：甲调查九年级30位同学植树情况统计表（单位：棵）
表2：乙调查三个年级各10位同学植树情况统计表（单位：棵）
根据以上材料回答下列问题：
（1）表1中30位同学植树情况的中位数是9 棵；
（2）已知表2的最后两列中有一个错误的数据，这个错误的数据是11 ，正确的数据应该是12
（3）指出哪位同学所抽取的样本能更好反映此次植树活动情况，并用该样本估计本次活动200位同学一共植树多少棵？
表1：甲调查九年级30位同学植树情况统计表（单位：棵）
| 每人植树情况 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 6 | 15 | 6 |
| 频率 | 0.1 | 0.2 | 0.5 | 0.2 |
| 每人植树情况 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 6 | 3 | 11 | 6 |
| 频率 | 0.1 | 0.2 | 0.1 | 0.4 | 0.2 |
（1）表1中30位同学植树情况的中位数是9 棵；
（2）已知表2的最后两列中有一个错误的数据，这个错误的数据是11 ，正确的数据应该是12
（3）指出哪位同学所抽取的样本能更好反映此次植树活动情况，并用该样本估计本次活动200位同学一共植树多少棵？
22．如图，在边长为1的正方形组成的5×8方格中，△ABC的顶点都在格点上．
（1）在给定的方格中，以直线AB为对称轴，画出△ABC的轴对称图形△AB
（1）在给定的方格中，以直线AB为对称轴，画出△ABC的轴对称图形△AB
| A． （2）求sin∠ABD的值．  |
23．如图，BF为⊙O的直径，直线AC交⊙O于A，B两点，点D在⊙O上，BD平分∠OBC，DE⊥AC于点
| A． （1）求证：直线DE是⊙O的切线； （2）若 BF=10，sin∠BDE=  ，求DE的长． |
24．在平面直角坐标系中，点A的坐标为（0，3），点B和点D的坐标分别为（m，0），（n，4），且m＞0，四边形ABCD是矩形．
（1）如图1，当四边形ABCD为正方形时，求m，n的值；
（2）在图2中，画出矩形ABCD，简要说明点C，D的位置是如何确定的，并直接用含m的代数式表示点C的坐标；
（3）探究：当m为何值时，矩形ABCD的对角线AC的长度最短．
（1）如图1，当四边形ABCD为正方形时，求m，n的值；
（2）在图2中，画出矩形ABCD，简要说明点C，D的位置是如何确定的，并直接用含m的代数式表示点C的坐标；
（3）探究：当m为何值时，矩形ABCD的对角线AC的长度最短．
25．如图，抛物线l：y=
（x﹣h）2﹣2与x轴交于A，B两点（点A在点B的左侧），将抛物线ι在x轴下方部分沿轴翻折，x轴上方的图象保持不变，就组成了函数ƒ的图象．
（1）若点A的坐标为（1，0）．
①求抛物线l的表达式，并直接写出当x为何值时，函数ƒ的值y随x的增大而增大；
②如图2，若过A点的直线交函数ƒ的图象于另外两点P，Q，且S△ABQ=2S△ABP，求点P的坐标；
（2）当2＜x＜3时，若函数f的值随x的增大而增大，直接写出h的取值范围．
（x﹣h）2﹣2与x轴交于A，B两点（点A在点B的左侧），将抛物线ι在x轴下方部分沿轴翻折，x轴上方的图象保持不变，就组成了函数ƒ的图象．（1）若点A的坐标为（1，0）．
①求抛物线l的表达式，并直接写出当x为何值时，函数ƒ的值y随x的增大而增大；
②如图2，若过A点的直线交函数ƒ的图象于另外两点P，Q，且S△ABQ=2S△ABP，求点P的坐标；
（2）当2＜x＜3时，若函数f的值随x的增大而增大，直接写出h的取值范围．
