全一卷
1.在 ,0,1,
,0,1, 四个数中,负数是( )
四个数中,负数是( )
 ,0,1,
,0,1, 四个数中,负数是( )
四个数中,负数是( )A. | B.0 | C.1 | D. |
2.浙江省陆域面积为101800平方千米,其中数据101800用科学记数法表示为( )
A. | B. | C. | D. |
3.如图是由4个大小相同的立方块搭成的几何体,这个几何体的主视图是( )


A. | B. | C. | D. |
4.下列计算正确的是( )
A. | B. | C. | D. |
5.在一个箱子里放有1个自球和2个红球,它们除颜色外其余都相同,从箱子里任意摸出1个球,摸到白球的概率是( )
| A.1 | B.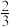 | C. | D. |
6.二次函数 图象的顶点坐标是( )
图象的顶点坐标是( )
 图象的顶点坐标是( )
图象的顶点坐标是( )A. | B. | C. | D. |
7.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒 ,
, 组成,两根棒在
组成,两根棒在 点相连并可绕
点相连并可绕 转动,
转动, 点固定,
点固定, ,点
,点 ,
, 可在槽中滑动,若
可在槽中滑动,若 ,则
,则 的度数是( )
的度数是( )

 ,
, 组成,两根棒在
组成,两根棒在 点相连并可绕
点相连并可绕 转动,
转动, 点固定,
点固定, ,点
,点 ,
, 可在槽中滑动,若
可在槽中滑动,若 ,则
,则 的度数是( )
的度数是( )
| A.60° | B.65° | C.75° | D.80° |
8.一块圆形宣传标志牌如图所示,点 ,
, ,
, 在
在 上,
上, 垂直平分
垂直平分 于点
于点 ,现测得
,现测得 ,
, ,则圆形标志牌的半径为( )
,则圆形标志牌的半径为( )

 ,
, ,
, 在
在 上,
上, 垂直平分
垂直平分 于点
于点 ,现测得
,现测得 ,
, ,则圆形标志牌的半径为( )
,则圆形标志牌的半径为( )
A. | B. | C. | D. |
9.如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为( )


| A.1 | B. | C. | D.2 |
10.如图,正方形 的边长为4,点
的边长为4,点 是
是 的中点,点
的中点,点 从点
从点 出发,沿
出发,沿 移动至终点
移动至终点 ,设
,设 点经过的路径长为
点经过的路径长为 ,
, 的面积为
的面积为 ,则下列图象能大致反映
,则下列图象能大致反映 与
与 函数关系的是( )
函数关系的是( )

 的边长为4,点
的边长为4,点 是
是 的中点,点
的中点,点 从点
从点 出发,沿
出发,沿 移动至终点
移动至终点 ,设
,设 点经过的路径长为
点经过的路径长为 ,
, 的面积为
的面积为 ,则下列图象能大致反映
,则下列图象能大致反映 与
与 函数关系的是( )
函数关系的是( )
A. | B. | C. | D. |
11.计算:
_____ .

12.数据2,7,5,7,9的众数是_____ .
13.已知实数 ,
, 满足
满足 ,则代数式
,则代数式 的值为
的值为_____ .
 ,
, 满足
满足 ,则代数式
,则代数式 的值为
的值为14.如图,人字梯 ,
, 的长都为2米.当
的长都为2米.当 时,人字梯顶端高地面的高度
时,人字梯顶端高地面的高度 是
是____ 米(结果精确到 .参考依据:
.参考依据: ,
, ,
, )
)

 ,
, 的长都为2米.当
的长都为2米.当 时,人字梯顶端高地面的高度
时,人字梯顶端高地面的高度 是
是 .参考依据:
.参考依据: ,
, ,
, )
)
15.如图,在平面直角坐标系中, 为坐标原点,
为坐标原点, 的边
的边 在
在 轴上,顶点
轴上,顶点 在
在 轴的正半轴上,点
轴的正半轴上,点 在第一象限,将
在第一象限,将 沿
沿 轴翻折,使点
轴翻折,使点 落在
落在 轴上的点
轴上的点 处,点
处,点 恰好为
恰好为 的中点,
的中点, 与
与 交于点
交于点 .若
.若
 图象经过点
图象经过点 ,且
,且 ,则
,则 的值为
的值为____ .

 为坐标原点,
为坐标原点, 的边
的边 在
在 轴上,顶点
轴上,顶点 在
在 轴的正半轴上,点
轴的正半轴上,点 在第一象限,将
在第一象限,将 沿
沿 轴翻折,使点
轴翻折,使点 落在
落在 轴上的点
轴上的点 处,点
处,点 恰好为
恰好为 的中点,
的中点, 与
与 交于点
交于点 .若
.若
 图象经过点
图象经过点 ,且
,且 ,则
,则 的值为
的值为
16.如图,由两个长为2,宽为1的长方形组成“7”字图形.

(1)将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形 ,其中顶点
,其中顶点 位于
位于 轴上,顶点
轴上,顶点 ,
, 位于
位于 轴上,
轴上, 为坐标原点,则
为坐标原点,则 的值为____.
的值为____.
(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点 ,摆放第三个“7”字图形得顶点
,摆放第三个“7”字图形得顶点 ,依此类推,…,摆放第
,依此类推,…,摆放第 个“7”字图形得顶点
个“7”字图形得顶点 ,…,则顶点
,…,则顶点 的坐标为_____.
的坐标为_____.

(1)将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形
 ,其中顶点
,其中顶点 位于
位于 轴上,顶点
轴上,顶点 ,
, 位于
位于 轴上,
轴上, 为坐标原点,则
为坐标原点,则 的值为____.
的值为____.(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点
 ,摆放第三个“7”字图形得顶点
,摆放第三个“7”字图形得顶点 ,依此类推,…,摆放第
,依此类推,…,摆放第 个“7”字图形得顶点
个“7”字图形得顶点 ,…,则顶点
,…,则顶点 的坐标为_____.
的坐标为_____.17.计算:

18.已知:如图,在菱形 中,点
中,点 ,
, 分别在边
分别在边 ,
, 上,且
上,且 ,连结
,连结 ,
, .求证:
.求证: .
.

 中,点
中,点 ,
, 分别在边
分别在边 ,
, 上,且
上,且 ,连结
,连结 ,
, .求证:
.求证: .
.
19.如图,在 的方格子中,
的方格子中, 的三个顶点都在格点上,
的三个顶点都在格点上,

(1)在图1中画出线段 ,使
,使 ,其中
,其中 是格点,
是格点,
(2)在图2中画出平行四边形 ,其中
,其中 是格点.
是格点.
 的方格子中,
的方格子中, 的三个顶点都在格点上,
的三个顶点都在格点上,
(1)在图1中画出线段
 ,使
,使 ,其中
,其中 是格点,
是格点,(2)在图2中画出平行四边形
 ,其中
,其中 是格点.
是格点.20.某校为积极响应“南孔圣地,衢州有礼”城市品牌建设,在每周五下午第三节课开展了丰富多彩的走班选课活动.其中综合实践类共开设了“礼行”“礼知”“礼思”“礼艺”“礼源”等五门课程,要求全校学生必须参与其中一门课程.为了解学生参与综合实践类课程活动情况,随机抽取了部分学生进行调查,根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图.

(1)请问被随机抽取的学生共有多少名?并补全条形统计图.
(2)在扇形统计图中,求选择“礼行”课程的学生人数所对应的扇形圆心角的度数.
(3)若该校共有学生1200人,估计其中参与“礼源”课程的学生共有多少人?

(1)请问被随机抽取的学生共有多少名?并补全条形统计图.
(2)在扇形统计图中,求选择“礼行”课程的学生人数所对应的扇形圆心角的度数.
(3)若该校共有学生1200人,估计其中参与“礼源”课程的学生共有多少人?
21.如图,在等腰 中,
中, ,以
,以 为直径作
为直径作 交
交 于点
于点 ,过点
,过点 作
作 ,垂足为
,垂足为 .
.

(1)求证: 是
是 的切线.
的切线.
(2)若 ,
, ,求
,求 的长.
的长.
 中,
中, ,以
,以 为直径作
为直径作 交
交 于点
于点 ,过点
,过点 作
作 ,垂足为
,垂足为 .
.
(1)求证:
 是
是 的切线.
的切线.(2)若
 ,
, ,求
,求 的长.
的长.22.某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数 (间)与每间标准房的价格
(间)与每间标准房的价格 (元)的数据如下表:
(元)的数据如下表:

(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求 关于
关于 的函数表达式、并写出自变量
的函数表达式、并写出自变量 的取值范围.
的取值范围.
(3)设客房的日营业额为 (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
 (间)与每间标准房的价格
(间)与每间标准房的价格 (元)的数据如下表:
(元)的数据如下表: (元) (元) | … | 190 | 200 | 210 | 220 | … |
 (间) (间) | … | 65 | 60 | 55 | 50 | … |

(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求
 关于
关于 的函数表达式、并写出自变量
的函数表达式、并写出自变量 的取值范围.
的取值范围.(3)设客房的日营业额为
 (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?23.定义:在平面直角坐标系中,对于任意两点 ,
, ,若点
,若点 满足
满足 ,
, ,那么称点
,那么称点 是点
是点 ,
, 的融合点.
的融合点.
例如: ,
, ,当点
,当点 满是
满是 ,
, 时,则点
时,则点 是点
是点 ,
, 的融合点,
的融合点,

(1)已知点 ,
, ,
, ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点 ,点
,点 是直线
是直线 上任意一点,点
上任意一点,点 是点
是点 ,
, 的融合点.
的融合点.
①试确定 与
与 的关系式.
的关系式.
②若直线 交
交 轴于点
轴于点 ,当
,当 为直角三角形时,求点
为直角三角形时,求点 的坐标.
的坐标.
 ,
, ,若点
,若点 满足
满足 ,
, ,那么称点
,那么称点 是点
是点 ,
, 的融合点.
的融合点.例如:
 ,
, ,当点
,当点 满是
满是 ,
, 时,则点
时,则点 是点
是点 ,
, 的融合点,
的融合点,
(1)已知点
 ,
, ,
, ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.(2)如图,点
 ,点
,点 是直线
是直线 上任意一点,点
上任意一点,点 是点
是点 ,
, 的融合点.
的融合点.①试确定
 与
与 的关系式.
的关系式.②若直线
 交
交 轴于点
轴于点 ,当
,当 为直角三角形时,求点
为直角三角形时,求点 的坐标.
的坐标.24.如图,在 中,
中, ,
,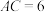 ,
, ,
, 平分
平分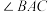 交
交 于点
于点 ,过点
,过点 作
作 交
交 于点
于点 ,点
,点 是线段
是线段 上的动点,连接
上的动点,连接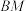 并延长分别交
并延长分别交 ,
, 于点
于点 、
、 .
.

(1)求 的长.
的长.
(2)若点 是线段
是线段 的中点,求
的中点,求 的值.
的值.
(3)请问当 的长满足什么条件时,在线段
的长满足什么条件时,在线段 上恰好只有一点
上恰好只有一点 ,使得
,使得 ?
?
 中,
中, ,
,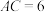 ,
, ,
, 平分
平分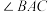 交
交 于点
于点 ,过点
,过点 作
作 交
交 于点
于点 ,点
,点 是线段
是线段 上的动点,连接
上的动点,连接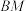 并延长分别交
并延长分别交 ,
, 于点
于点 、
、 .
.
(1)求
 的长.
的长.(2)若点
 是线段
是线段 的中点,求
的中点,求 的值.
的值.(3)请问当
 的长满足什么条件时,在线段
的长满足什么条件时,在线段 上恰好只有一点
上恰好只有一点 ,使得
,使得 ?
? 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
